Convergence d'une fonction d'intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ezril13
- Membre Naturel
- Messages: 16
- Enregistré le: 13 Sep 2013, 14:08
-
 par ezril13 » 03 Déc 2015, 19:39
par ezril13 » 03 Déc 2015, 19:39

Bonjour,
J'ai déjà fait les questions 1,2,3,4 et je bloque sur la 5.
Je ne vois pas comment utiliser l'expression de la question 4 pour déduire 5.
Vu la forme je pense qu'on doit s'en servir en prenant

mais je n'arrive pas à la faire apparaitre à cause du
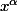
Comment faire?
Merci.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Déc 2015, 20:26
par Ben314 » 03 Déc 2015, 20:26
Salut,
Evidement, on intuite assez fort que, lorsque

tend vers 0, l'intégrale
=\int_0^1\frac{dx}{x^\alpha(1+\lambda x)})
va tendre vers

(à calculer).
Et pour montrer que c'est une bonne intuition, on regarde évidement la différence entre les deux :
=\int_0^1\frac{1}{x^\alpha}\Big(1-\frac{1}{1+ \lambda x}\Big)dx)
REt là, on risque de voir a quoi sert l'indiction...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
ezril13
- Membre Naturel
- Messages: 16
- Enregistré le: 13 Sep 2013, 14:08
-
 par ezril13 » 04 Déc 2015, 18:20
par ezril13 » 04 Déc 2015, 18:20
Ok merci, j'ai réussi à majorer et faire tendre vers 0.
En me relisant j'ai vu que ma question 2 ést fausse.
mon idée était de faire sortir
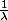
:
)
et d'essayer de minoré l'intégrale par quelque chose qui ne dépend pas de

Mais la je bloque.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 04 Déc 2015, 22:18
par Ben314 » 04 Déc 2015, 22:18
Pour montrer que l'intégrale tend vers l'infini, il faut la minorer (par un truc simple qui tend vers l'infini) donc sans doute minorer la fonction qu'on intègre, c'est à dire majorer le

du dénominateur.
Vu que

tend vers 0,

est effectivement "pas trop grand", mais à condition de ne pas prendre de valeurs de x trop grandes.
Donc je tenterais bien un truc du style

pour

qui conduit à écrire que :
}\geq \int_1^{\frac{1}{\lambda}}\frac{dx}{x^\alpha(1 + \lambda x)}\geq \int_1^{\frac{1}{\lambda}}\frac{dx}{2x^\alpha})
Et ça permet effectivement de conclure.
Y'a peut-être plus simple...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités

