Suite et trigonométrie

par **Clemo** » 21 Nov 2015, 17:10

Bonjour, pouvez vous m'aider à résoudre cet exercice svp:

Dans cet exercice, dire si la proposition est vraie ou fausse et justifier.

Soit (Un) la suite définie pour tout n ;) N, par Un=(-1)^n+2*sin[(;)/4)*n]

a. Pour tout entier n, on a: Un+8 (n+8 en indice)>Un
b. Pour tout entier naturel n, on a: -3;)Un;)3
c. La suite Un est monotone.
d. lim (n;)+;)) (Un)/n = 0

En vous remerciant, je suis pommé...

par **titine** » 21 Nov 2015, 18:15

Clemo a écrit:Bonjour, pouvez vous m'aider à résoudre cet exercice svp:

Dans cet exercice, dire si la proposition est vraie ou fausse et justifier.

Soit (Un) la suite définie pour tout n N, par Un=(-1)^n+2*sin[(;)/4)*n]

a. Pour tout entier n, on a: Un+8 (n+8 en indice)>Un

U(n+8) = (-1)^(n+8) + 2*sin[(pi/4)*(n+8)] = (-1)^(n+8) + 2*sin[(pi/4)*n + 2pi] = (-1)^(n+8) + 2*sin[(pi/4)*n]
Si n est pair alors (n+8) est pair aussi donc (-1)^n = 1 et (-1)^(n+8) = 1. Donc U(n+8) = U(n)
Si n est impair alors (n+8) aussi donc (-1)^n = -1 et (-1)^(n+8) = -1. Donc U(n+8) = U(n)
Donc dans tous les cas U(n+8) = U(n)

b) -1

sin[(pi/4)*n]

1
Donc -2

2*sin[(pi/4)*n]

2
De plus -1

(-1)^n

1 car (-1)^n est égal à -1 ou 1
Donc -3

(-1)^n + 2*sin[(pi/4)*n]

3

par **Clemo** » 22 Nov 2015, 11:24

Merci pour votre réponse, elle m'est très utile...

Pour montrer que la suite est monotone ou pas, j'ai voulu la tracé sur geogebra mais ça na pas marché comment dois-je faire?

En vous remerciant.

par **biss** » 22 Nov 2015, 12:07

la suite n'est pas monotone car c'est le produit de fonction non monotone
et le fait d avoir Un+8=Un le confirme aussi

par **Clemo** » 22 Nov 2015, 12:30

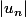
P'tipito a écrit:Et pour la limite, il suffit de regarder pour et de majorer par 1

Comment ça?

par **Clemo** » 22 Nov 2015, 12:55

P'tipito a écrit:Tu sais que
Tu sais aussi que |sin|
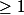
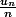
du coup qui tend vers 0 donc avec le théorème des gendarmes tend vers 0 donc aussi

Je ne comprend pas est-il possible de m'expliquer d'une autre manière?

par **Clemo** » 25 Nov 2015, 14:33

Pouvez-vous m'aider svp?

par **Clemo** » 26 Nov 2015, 17:01

P'tipito a écrit:Salut, désolé, j'étais un peu occupé ces derniers jours. Bon déjà y avait une erreur, |sin| est plus petit ou égale à 1 (pas plus grand). J'ai corrigé.
Qu'est-ce que tu ne comprends pas exactement?

Bah tout...

par **biss** » 26 Nov 2015, 17:14

Clemo a écrit:Bah tout...

Quelle est la plus grande valeur de

? La plus petite ?
Quelle est la plus grande valeur de

? La plus petite ?
Quelle est alors l'encadrement de

? De

? Quand n tend vers +00 ?

Suite et trigonométrie

Suite et trigonométrie

Qui est en ligne