Calculer
Au boulot!!
4 messages
- Page 1 sur 1
au boulot!!
par jlb » 21 Nov 2015, 18:38
Bon, je suis tombé sur ce petit exo sympa. A vous de jouer!
Calculerdx}{1+x^2})
Calculer
par zygomatique » 21 Nov 2015, 18:48
salut
changement de variable
:ptdr:
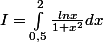
changement de variable
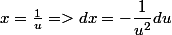
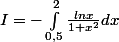
:ptdr:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
par aymanemaysae » 21 Nov 2015, 19:07
Comme vous l'avez indiqué:
I = intégrale{(1/2 à 2) Ln(x)/(1+x^2) dx} = - intégrale{(1/2 à 2) Ln(u)/(1+u^2) du},
donc 2 I = 0 , donc I = 0 .
J'espère que c'est le résultat recherché.
I = intégrale{(1/2 à 2) Ln(x)/(1+x^2) dx} = - intégrale{(1/2 à 2) Ln(u)/(1+u^2) du},
donc 2 I = 0 , donc I = 0 .
J'espère que c'est le résultat recherché.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :