Algebre lineaire, vecteurs libres et liés etc
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 20 Nov 2015, 01:56
par ArtyB » 20 Nov 2015, 01:56
Bonjour,
Petite mise en jambe après une longue période privé d'algèbre linéaire, c'est dur de s'y remettre, parce que j'ai un peut tout oublié.
Lorsque l'on a une famille de vecteurs libres, si l'on veut déterminer la dimension du sous espace vectoriel formé par ces vecteurs, on fait comment ? J'ai essayé de trouver des exemples sur Internet mais j'ai l'impression que tout le monde dit des choses différentes (je sais bien qu'il y a plusieurs façons de faire les choses mais bon).
Par exemple, si j'ai ces trois vecteurs là:
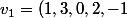,\ v_{2}=(2,-2,1,0,1),\ v_{3}=(3,-3,1,0,0))
Cette famille est libre, et intuitivement je dirai que la dimension de la base F formée de ces trois vecteurs est 3, mais comment le démontrer ?
Et lorsque l'on demande "combien d'équations linéaires sont nécessaires pour définir le sous espace vectoriel ?" qu'est-ce que cela signifie ?
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
 par Matt_01 » 20 Nov 2015, 02:21
par Matt_01 » 20 Nov 2015, 02:21
La dimension de l'espace vectoriel est effectivement 3.
Pour le "prouver" il faut voir comment tu définies la dimension. Pour moi c'est le cardinal d'une base de l'espace vectoriel en question (ce nombre ne change pas selon la base). Vu que par définition, ta famille est une base de ton sous espace vectoriel, la dimension de l'espace vectoriel est 3.
Une manière de définir ton espace vectoriel avec des équations linéaires consiste à le définir comme l'ensemble des solutions d'un système linéaire, et donc comme le noyau d'une matrice n*5 non nulle.
Vu que la dimension de l'ev est 5 et que tu as un sev F de dimension 3, F orthogonal est de dimension 2 de base disons X et Y.
La matrice 2*5 formée des lignes X et Y a pour noyau F.
Il te suffit donc de deux équations linéaires, et ces équations sont en fait X.u = 0 et Y.u = 0
-
pianojo
- Membre Naturel
- Messages: 50
- Enregistré le: 19 Nov 2015, 13:16
-
 par pianojo » 20 Nov 2015, 02:37
par pianojo » 20 Nov 2015, 02:37
Le déterminant de la matrice formée des vecteurs (1,0,0,0,0), (0,1,0,0,0), v1, v2 et v3 vaut 2 (immédiat grâce à tous les 0). Il est non nul donc on a trouvé une base de ton ev de dimension 5. En retirant les 2 vecteurs qu'on a ajoutés, il te reste forcément un sous-ev de dimension 5-2=3 (généré par une combinaison linéaire de 3 vecteurs d'une quelconque de ses bases).
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 20 Nov 2015, 20:24
par ArtyB » 20 Nov 2015, 20:24
D'accord pour la dimension, merci, c'est assez simple donc.
@ Matt
Concernant les équations, je n'ai en revanche pas tout compris.
"comme le noyau d'une matrice n*5 non nulle." pourquoi cela ?
On vient de dire que F était de base 3 pourquoi est-ce qu'il est de base 2 maintenant ?
Je ne comprends pas du tout le raisonnement, dans mes souvenirs on faisait ça de manière plus simple...
-
pianojo
- Membre Naturel
- Messages: 50
- Enregistré le: 19 Nov 2015, 13:16
-
 par pianojo » 20 Nov 2015, 20:31
par pianojo » 20 Nov 2015, 20:31
Dans sa réponse, F est bien de dimension 3. C'est l'orthogonal de F qui est de dimension 2 (le reste des dimensions).
Cela reste simple : 3 vecteurs indépendants définissent ton sous espace F de dimension 3, et 2 autres définissent l'espace orthogonal.
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 20 Nov 2015, 21:04
par ArtyB » 20 Nov 2015, 21:04
Ah, au temps pour moi, je comprends mieux. Mais je ne vois pas le rapport avec les équations définissant un sous espace vectoriel, qu'est-ce cela veut dire des équations qui définissent un sev ? Et comment les trouver ?
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
 par Matt_01 » 20 Nov 2015, 23:02
par Matt_01 » 20 Nov 2015, 23:02
Ben pour moi, "définir un sev avec des équations" c'est trouver un ensemble d'équations linéaires S tel que "u vérifie S" <=> "u appartient à F".
Et si tu prends une base (e_i) de l'orthogonal de F, S formé des équations e_i.u = 0 convient (e_i.u = 0 pour tout i ssi u appartient à l'orthogonal de l'orthogonal de F, qui est F).
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 21 Nov 2015, 03:23
par ArtyB » 21 Nov 2015, 03:23
" tel que "u vérifie S" <=> "u appartient à F". "
Qu'est-ce que u ici ?
De même pour e_i.u ?
-
pianojo
- Membre Naturel
- Messages: 50
- Enregistré le: 19 Nov 2015, 13:16
-
 par pianojo » 21 Nov 2015, 11:35
par pianojo » 21 Nov 2015, 11:35
Ne te complique pas la vie, et raisonne avec les vecteurs. Prendre un ensemble de relations linéaires veut juste dire prendre des vecteurs (la base) dont les combinaisons (linéaires) forment l'espace vectoriel.
Tel que je comprends ce qui a été écrit, u est un vecteur et S un ensemble de relations linéaires.
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 21 Nov 2015, 12:56
par ArtyB » 21 Nov 2015, 12:56
Donc j'ai juste à trouver des vecteurs qui génèrent le sev c'est ça ?
-
pianojo
- Membre Naturel
- Messages: 50
- Enregistré le: 19 Nov 2015, 13:16
-
 par pianojo » 21 Nov 2015, 13:06
par pianojo » 21 Nov 2015, 13:06
Des vecteurs indépendants, oui (tu ne dois pas pouvoir exprimer un vecteur comme combinaison linéaire des autres). Si tu prends deux vecteurs parallèles par exemple, l'espace engendré par eux est de dimension 1 et non 2.
-
pianojo
- Membre Naturel
- Messages: 50
- Enregistré le: 19 Nov 2015, 13:16
-
 par pianojo » 21 Nov 2015, 13:14
par pianojo » 21 Nov 2015, 13:14
Le déterminant est souvent pratique, car il non nul si tous les vecteurs sont indépendants. Par contre, ce n'est applicable qu'à n vecteurs de n variables. Si tu as moins de n vecteurs, par exemple n-2, et que tu trouves 2 vecteurs supplémentaires qui avec les autres te donnent un déterminant non nul, tu as montré que tes n-2 vecteurs sont indépendants. Par contre, trouver les dépendances si tu tombes sur 0 peut être casse-pied parfois, en particulier quand les vecteurs sont un peu long. Cherche sur internet : comment trouver le rang d'une matrice.
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 21 Nov 2015, 16:43
par ArtyB » 21 Nov 2015, 16:43
D'accord, donc si j'ai bien compris:
Si v=(x,y,z) est un vecteur du sev engendré par les vecteurs v1, v2 et v3 alors v est une combinaison linéaire des vecteurs v1, v2, et v3 telle que:
v=av1+bv2+cv3
soit:
x=a+2b+3c
y=3a-2b-3c
z=b+c
t=2a
u=-a+b
On résout le système et on trouve que:
a=t/2
b=u+t/2
c=z-u-t/2
y=u-t-3z (1)
x=-u-t+3z (2)
Donc v est de la forme (-u+3z-t,u-t+3z,z,t,u) et je peux prendre les équations (1) et (2) pour définir F, c'est bien cela ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
