Valeurs propres

[C.l]

Bonsoir,

je ne comprend pas comment faire agir l'opérateur Hamiltonien sur une fonction pour savoir s'il s'agit bien d'une fonction propre de l'opérateur

car il y a une formule avec:

-h^2/(2m) * d^2/(x^2) + 1/2*k*x^2

Alors si je fais la dérivée seconde de ma fonction je la multiplie par -h^2/(2m) ?

Mais avec le 1/2*k*x^2 que cela signifie?

Merci d'avance :-)

[Skullkid]

L'opérateur position agit en multipliant par la position, donc dans ton cas tu multiplies par 1/2*k*x^2.

[C.l]

L'opérateur position agit en multipliant par la position, donc dans ton cas tu multiplies par 1/2*k*x^2.

Oui sauf qu'après je ne trouve pas de valeur propre car k n'apparait pas dans le premier terme de la formule....??

[Skullkid]

Pour trouver les valeurs propres tu dois en principe résoudre l'équa diff 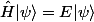. Dans ton cas particulier on peut s'en sortir sans la résoudre explicitement en introduisant des opérateurs de création/annihilation, tu peux trouver la résolution détaillée un peu partout sur internet en cherchant "oscillateur harmonique quantique".

[C.l]

Pour trouver les valeurs propres tu dois en principe résoudre l'équa diff . Dans ton cas particulier on peut s'en sortir sans la résoudre explicitement en introduisant des opérateurs de création/annihilation, tu peux trouver la résolution détaillée un peu partout sur internet en cherchant "oscillateur harmonique quantique".

C'est très gentil d'avoir répondu à ma question... Justement j'ai cherché partout mais j'ai rien trouver qui montre vraiment comment cet opérateur "attaque" la fonction

[Skullkid]

Pour l'opérateur je t'ai déjà répondu : le premier terme dérive deux fois par rapport à la position, le deuxième terme multiplie par 1/2*k*x^2 (sinon tu es censé avoir un cours qui explique ces choses-là). Quant au reste, tout est détaillé dans le premier résultat Google pour "oscillateur harmonique quantique", j'ai donc du mal à croire que tu aies cherché partout...