Fonction exponentielle
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
damajuma
- Membre Relatif
- Messages: 113
- Enregistré le: 21 Juil 2015, 13:10
-
 par damajuma » 15 Nov 2015, 17:52
par damajuma » 15 Nov 2015, 17:52
dsl mais je ne comprend pas.
on me demande de montrer que

-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 15 Nov 2015, 17:56
par Carpate » 15 Nov 2015, 17:56
damajuma a écrit:dsl mais je ne comprend pas.
on me demande de montrer que

Tu ne vois pas la contradiction ?
Comment x pourrait être égal à x puisqu'il lui est toujours inférieur
Je te rappelle que tu as montré que tout réel

vérifie

et non

!
-
damajuma
- Membre Relatif
- Messages: 113
- Enregistré le: 21 Juil 2015, 13:10
-
 par damajuma » 15 Nov 2015, 17:58
par damajuma » 15 Nov 2015, 17:58
justement je ne doit pas montrer qu'il lui est égal je doit montrer qu'il lui est different
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 15 Nov 2015, 18:04
par Carpate » 15 Nov 2015, 18:04
damajuma a écrit:justement je ne doit pas montrer qu'il lui est égal je doit montrer qu'il lui est different
Tu m'as mal lu. Je n'ai pas dit que x était égal à
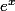
mais fait l'hypothése qu'il était égal à x et que cette hypothèse était en contradiction avec l'inégalité

donc x ne peut pas être égal à

-
damajuma
- Membre Relatif
- Messages: 113
- Enregistré le: 21 Juil 2015, 13:10
-
 par damajuma » 15 Nov 2015, 18:08
par damajuma » 15 Nov 2015, 18:08
ha ok c'est bon

pour la 3a la deriver on la calcul aussi avec
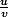
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 15 Nov 2015, 18:12
par Carpate » 15 Nov 2015, 18:12
damajuma a écrit:ha ok c'est bon

pour la 3a la deriver on la calcul aussi avec
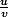
la dérivée !
Ben oui, tu vois une autre formule possible ...
-
damajuma
- Membre Relatif
- Messages: 113
- Enregistré le: 21 Juil 2015, 13:10
-
 par damajuma » 15 Nov 2015, 18:15
par damajuma » 15 Nov 2015, 18:15
je trouve
^2})
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 15 Nov 2015, 18:26
par Carpate » 15 Nov 2015, 18:26
damajuma a écrit:je trouve
^2})
Non, je trouve
^2})
-
damajuma
- Membre Relatif
- Messages: 113
- Enregistré le: 21 Juil 2015, 13:10
-
 par damajuma » 15 Nov 2015, 18:31
par damajuma » 15 Nov 2015, 18:31
 - e^x*(e^x-1)}{(e^x-x)^2})
est ça c'est bon ?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 15 Nov 2015, 18:31
par Carpate » 15 Nov 2015, 18:31
damajuma a écrit: - e^x*(e^x-1)}{(e^x-x)^2})
est ça c'est bon ?
Et si tu développais ?
-
damajuma
- Membre Relatif
- Messages: 113
- Enregistré le: 21 Juil 2015, 13:10
-
 par damajuma » 15 Nov 2015, 18:34
par damajuma » 15 Nov 2015, 18:34
^2})
c'est la que c'est faut je pense
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 15 Nov 2015, 18:39
par Carpate » 15 Nov 2015, 18:39
damajuma a écrit:^2})
c'est la que c'est faut je pense
Non, c'est OK et

ça donne ....
Attention e^x^2 donne
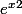
e^{x^2} donne
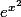
-
damajuma
- Membre Relatif
- Messages: 113
- Enregistré le: 21 Juil 2015, 13:10
-
 par damajuma » 15 Nov 2015, 18:42
par damajuma » 15 Nov 2015, 18:42
ha ok dsl petite erreur de code


je penser que cela sannulait car il y en a un positif et un negatif
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 15 Nov 2015, 18:42
par Carpate » 15 Nov 2015, 18:42
damajuma a écrit:^2})
c'est la que c'est faut je pense
Ah excuse
Tu as raison donc la dérivée est
}{(e^x-x)^2)
-
damajuma
- Membre Relatif
- Messages: 113
- Enregistré le: 21 Juil 2015, 13:10
-
 par damajuma » 15 Nov 2015, 18:47
par damajuma » 15 Nov 2015, 18:47
est

cela sannule aussi non
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 15 Nov 2015, 18:53
par Carpate » 15 Nov 2015, 18:53
damajuma a écrit:est

cela sannule aussi non
'=\frac{(e^x-x)e^x-e^x(e^x-1)}{(e^x-x)^2}=\frac{e^{2x}-xe^x-e^{2x}+e^x}{(e^x-x)^2}=\frac{-x^e^x+e^x}{(e^x-x)^2}=\frac{e^x(1-x)}{(e^x-x)^2})
-
damajuma
- Membre Relatif
- Messages: 113
- Enregistré le: 21 Juil 2015, 13:10
-
 par damajuma » 15 Nov 2015, 18:56
par damajuma » 15 Nov 2015, 18:56
donc c'est encore dans le développement que je me suis tromper.
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 15 Nov 2015, 18:58
par Carpate » 15 Nov 2015, 18:58
damajuma a écrit:donc c'est encore dans le développement que je me suis tromper.
Donc on est d'accord pour la dérivée ...
Et tu t'es encore trompé dans trompe
r !
-
damajuma
- Membre Relatif
- Messages: 113
- Enregistré le: 21 Juil 2015, 13:10
-
 par damajuma » 15 Nov 2015, 19:00
par damajuma » 15 Nov 2015, 19:00
est pour la 3b c'est le même principe que pour la 2a il faut la faire en fonction des variations et du signe
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 15 Nov 2015, 19:04
par Carpate » 15 Nov 2015, 19:04
damajuma a écrit:est pour la 3b c'est le même principe que pour la 2a il faut la faire en fonction des variations et du signe
Tout à fait !
Je pensais que tu avais déjà fini ...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
