Fonction exponentielle

par **damajuma** » 15 Nov 2015, 16:00

Bonjour j'ai un DM a faire et je n'y arrive pas.

Soit q la fonction définie sur

par
q(x) =

1. Etudier les variations de q.
2. a) Montrer que, pour tout réel x, on a : q(x) =0, alors on a 1

f(x)

Merci pour vos reponse.

par **Carpate** » 15 Nov 2015, 16:24

damajuma a écrit:Bonjour j'ai un DM a faire et je n'y arrive pas.

Soit q la fonction définie sur par
q(x) =

1. Etudier les variations de q.
2. a) Montrer que, pour tout réel x, on a : q(x) =0, alors on a 1 f(x)

Merci pour vos reponse.

Merci pour vos reponse.

Encore faudrait-il qu'il ait eu des questions !

par **damajuma** » 15 Nov 2015, 16:29

déjà pour la derivée j'ai trouvé

est ce que c'est correct ?
et pour la 2a et 2b je ne vois pas comment faire.

par **Carpate** » 15 Nov 2015, 16:32

damajuma a écrit:déjà pour la derivée j'ai trouvé est ce que c'est correct ?
et pour la 2a et 2b je ne vois pas comment faire.

Non, c'est

par **damajuma** » 15 Nov 2015, 16:34

je l'ai calculer avec la formule

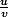
c'est bien ça ?

par **Carpate** » 15 Nov 2015, 16:51

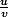
damajuma a écrit:je l'ai calculer avec la formule c'est bien ça ?

c'est le

qui ne va pas
Donne tes calculs intermédiaires

par **damajuma** » 15 Nov 2015, 16:58

oui je sais mais comment est tu arriver a ce resultat je n'y parvient pas

par **Carpate** » 15 Nov 2015, 17:01

damajuma a écrit:oui je sais mais comment est tu arriver a ce resultat je n'y parvient pas

par **damajuma** » 15 Nov 2015, 17:02

par **Carpate** » 15 Nov 2015, 17:04

damajuma a écrit:

Oui, donc on trouve le même résultat ...

par **damajuma** » 15 Nov 2015, 17:10

ok et apres pour la 2a est ce que je doit résoudre une ineqution

et la 2b je ne comprend pas

par **Carpate** » 15 Nov 2015, 17:12

damajuma a écrit:ok et apres pour la 2a est ce que je doit résoudre une ineqution
et la 2b je ne comprend pas

Non, la 2a) est la conséquence de la 1)
Qu'as-tu trouvé pour les variations de q(x) ?

par **damajuma** » 15 Nov 2015, 17:15

g trouver quel était croissante puit décroissante

par **Carpate** » 15 Nov 2015, 17:19

damajuma a écrit:g trouver quel était croissante puit décroissante

g trouver

évite le langage sms (et puis l'orthographe !)
Donc q(x) passe par un maximum (qui vaut ... pour x = ...)
Il suffit de le comparer à 1 pour répondre à la question 2a) ....

par **damajuma** » 15 Nov 2015, 17:22

ok desoler pour le language sms ça viens tous seul ;)
donc pour la 2a c juste de la lecture du tableau ok
et pour la 2b

par **Carpate** » 15 Nov 2015, 17:30

damajuma a écrit:ok desoler pour le language sms ça viens tous seul
donc pour la 2a c juste de la lecture du tableau ok
et pour la 2b

Je suppose que x=/= e^(x) signifie

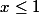
Pour tout réel

,

, si tu multiplies les 2 membres de l'inégalité par e^x, est-ce que cela change son sens et pourquoi ?

par **damajuma** » 15 Nov 2015, 17:32

non x=/=e^(x) signifie

(je l'ai modifier trop tard dsl)

par **Carpate** » 15 Nov 2015, 17:37

damajuma a écrit:non x=/=e^(x) signifie (je l'ai modifier trop tard dsl)

C'est la conséquence de l'inégalité stricte, sur R :

PS

je l'ai modifier trop tard

C'est agaçant ces infinitifs systématiques à la place d'un participe passé

par **damajuma** » 15 Nov 2015, 17:42

si je multiplie les deux cotés de l'inéquation prt e^(x) cela me donne

ce qui donne

Mais je ne voit pas en quoi cela repond a la question 2b

par **Carpate** » 15 Nov 2015, 17:49

damajuma a écrit:si je multiplie les deux cotés de l'inéquation prt e^(x) cela me donne ce qui donne
Mais je ne voit pas en quoi cela repond a la question 2b

Supposons qu'il existe une valeur de

telle que

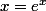
, il y a contradiction avec l'inégalité stricte valable pour tout x :

Fonction exponentielle

fonction exponentielle

Qui est en ligne