Limite fonction trigonométrique

[Kyg]

Bonjour,

Je n'arrive pas à trouver la limite en 0 de la fonction définie de 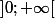dans par

[Suzet]

Il suffit de majorer la valeur absolue de ta fonction par x, et de conclure via le théorème des gendarmes, en faisant tendre x vers 0 par valeurs positives.

[zygomatique]

salut

la fonction sin est bornée ...

[aymanemaysae]

La fonction x sin(1/x) est définie sur R*, et comme sur ce domaine on a :
-1<= sin(1/x)<=1 <---> -x<= x sin(1/x)<= x , et comme lim(x-->0) x = 0 , donc par le théorème des
gendarmes on a : lim(x-->0) <= lim(x-->0) x sin(1/x) <= lim(x-->0) x
<--> 0 <= lim(x-->0) x sin(1/x) <= 0 <--> lim(x-->0) x sin(1/x) = 0 .

[Robot]

Extrait de la charte :

Lorsqu'un correcteur donne ipso facto la réponse complète à un élève sans que celui-ci n'ait fourni un effort de recherche ou ne paraisse complètement perdu, il est convenu que le modérateur le prévienne par message privé de son comportement contraire à la charte. Au delà de 3 manquements à la charte, le correcteur peut alors se voir sanctionner sous la forme d'une exclusion temporaire de 15 jours ou définitive si le correcteur ne modifie toujours pas son comportement.

[Lostounet]

@Aymanemaysae: La modération a supprimé votre message qui comportait une résolution complète de l'exercice. Merci de ne donner que des indications la prochaine fois.

[aymanemaysae]

Je m'excuse, je n'avais pas fait attention à ce point. Si c'est possible, est ce que je peux savoir combien de temps dois-je attendre pour donner la réponse si l'intéressé ne se manifeste pas?

[Lostounet]

Je m'excuse, je n'avais pas fait attention à ce point. Si c'est possible, est ce que je peux savoir combien de temps dois-je attendre pour donner la réponse si l'intéressé ne se manifeste pas?

Tu pourrais par exemple proposer ceci (ton message supprimé):

La fonction x sin(1/x) est définie sur R*, et comme sur ce domaine on a :
-1 -x0) x = 0 , donc par le théorème des
gendarmes (on peut conclure)

NB: Un autre modérateur a voulu t'exclure pendant quelques jours mais après négociation, ce sera le dernier avertissement pour cette fois. (on t'aime bien)

[Carpate]

Je m'excuse, je n'avais pas fait attention à ce point. Si c'est possible, est ce que je peux savoir combien de temps dois-je attendre pour donner la réponse si l'intéressé ne se manifeste pas?

C'est vrai que c'est frustrant quand on n'a pas de réponse à une indication ou à un message.
Certains sites permettent de voir si l'intéressé a lu le message.
Il faut avoir assez de détachement vis à vis de l'aide que l'on apporte ...

[Kyg]

Je suis désolée je n'avais pas vu toutes vos réponses. En tout cas merci, je n'avais pas du tout pensé à faire ça et c'était finalement très élémentaire.