Limite de suite

[claudy]

Bonjour

Dans un exercice j'ai prouvé que lim

Je veux maintenant calculer lim

J'ai pensé à poser n=2p^2

Donc le premier résultat donne lim
Et en simplifiant on peut déduire lim

Sauf que je n'ai toujours pas ce que je veux en indice. Il manque un "-1"
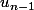
Peut on faire l'approximation que lim = lim ?

Merci de votre aide

[Doraki]

Non, tu ne peux pas vraiment évaluer la proximité de u(2n²+1) avec u(2n²) sans connaître quelquechose sur u.
D'ailleurs, lim un = lim u(n+1) = 0, mais ça ne va pas t'aider.

Par contre, tu peux plus facilement comparer sqrt(2n²-1) avec sqrt(2n²).


lim sqrt(n) un = a donc lim sqrt(2n²-1)u(2n²-1) = a ((2n²-1) est une suite d'entiers qui tend vers l'infini donc c'est juste une suite extraite de la première suite)

Maintenant tu n'as plus qu'à voir si lim sqrt(2n²-1)/n existe et si oui, la calculer.

[claudy]

Je comprends qu'on puisse écrire ça : lim sqrt(2n²-1)u(2n²-1) = a

Mais après je ne comprends pas vraiment ce qu'il faut faire