Convergence uniforme

[zaidoun]

Bonjour,

J'ai du mal à comprendre cette phrase:

" Lorsque h converge uniformément vers 0, alors par continuité de f(x, h) en h, on a que

la fonction t---> f(g(t), h(t)) converge uniformément vers la fonction f(g(t), 0)."

(f est une fonction continue de R^2 dans R).

Pouvez m'expliquer encore ça?

Merci d'avance.

[Robot]

C'est faux, sans hypothèses plus précises que tu as peut-être oublié de mentionner. D'où cela vient-il ?

[zaidoun]

voir ce lien page 9 iii): http://webusers.imj-prg.fr/~gregory.ginot/LM360/Corrige-TD7-LM360.pdf

et l'énoncé http://webusers.imj-prg.fr/~gregory.ginot/LM360/TD7-LM360.pdf (exercice 9).

[Robot]

Bon, je ne vais pas passer mon temps à éplucher des corrigés, mais voici un contre-exemple :
Soit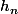 la fonction constante 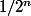sur . Elle converge uniformément vers la fonction nulle quand tend vers l'infini.
Soit l'identité de dans et .
Alors ne converge pas uniformément vers quand tend vers l'infini.

A toi de voir s'il y a dans l'exercice des hypothèses supplémentaires qui ne sont pas satisfaites par ce contre exemple.

[zaidoun]

Il n'y a pas des hypothèses supplémentaires, vraiment c'est étonnant!!!!!!!!!!!!!!!!!!!!!!!!

Quel est le problème?? La correction, peut être, n'est pas bonne?????????

[Robot]

Que veux-tu que je te dise ? S'il n'y a pas d'autre hypothèse et que le contre-exemple te convainc, c'est que le corrigé est fautif.

[El_Gato]

Il n'y a pas des hypothèses supplémentaires, vraiment c'est étonnant!!!!!!!!!!!!!!!!!!!!!!!!

Quel est le problème?? La correction, peut être, n'est pas bonne?????????

Non, le corrigé est bon. Le problème c'est que, dans l'exemple de ton exercice, l'espace de départ [0,1] est compact, ce qui n'est pas le cas de l'exemple donné par Robot.

[Robot]

Alors Zaidoun, tu vois bien qu'il y avait une hypothèse supplémentaire que tu me cachais !

[zaidoun]

Désolé Robot, j'ai pas fait attention à cette donnée.

Pouvez vous m'expliquer ou détailler de plus la correction, car j'ai pas bien saisi le corrigé.!!!!!!

[Robot]

Montre que les images de par les fonctions (au moins pour assez grand) sont contenues dans un compact. Ca nécessite que soit continue, hypothèse que tu n'as pas mentionnée. Conclus en utilisant la continuité uniforme de sur ce compact.

[zygomatique]

salut

ça veut dire quoi ::

Lorsque h converge uniformément vers 0

??

[Robot]

Lorsque h tend vers la fonction nulle pour la norme de la convergence uniforme

[MouLou]

J'avoue que j'ai aussi du mal. Il manque pas un indice?

[Robot]

Tout y est - sauf la résolution complète, bien sûr. Mais je laisse le plaisir de la trouver.

[MouLou]

Non je parle de la citation de Zygomatique, comment une fonction converge uniformément? Apres j'ai pas lu le corrigé, peut etre que la correction de la coquille est immédiate.

Edit: ok faut juste remplacer h par une suite

[Robot]

Je l'ai fait par commodité, mais ce n'est pas nécessaire. Et ce n'est pas une coquille à mon sens. Pas plus que dans l'expression "quand x tend vers 0". Comme je l'ai déjà écrit (l'as-tu vu ?), ici c'est "quand h tend vers 0 pour la norme de la convergence uniforme".

[zygomatique]

oui j'avais pas saisi en terme de fonction bien sur ... merci Robot ... (et en plus tu le reprécisais dans ton deuxième post) ....

[zaidoun]

Montre que les images de par les fonctions (au moins pour assez grand) sont contenues dans un compact. Ca nécessite que soit continue, hypothèse que tu n'as pas mentionnée. Conclus en utilisant la continuité uniforme de sur ce compact.

Encore j'ai pas bien compris votre réponse.Pouvez vous me donner quel résultat ou quel outil vous avez utilisé ici?

[Robot]

L'image d'un compact par une fonction continue est compacte, et une fonction continue sur un compact est uniformément continue sur ce compact.

[zaidoun]

L'image d'un compact par une fonction continue est compacte, et une fonction continue sur un compact est uniformément continue sur ce compact.

Salut Robot,

Pouvez vous me corriger ce raisonnement:

Les fonctions g et h sont continues sur [0,1], alors g([0,1]) et h([0,1]) sont inclus respectivement dans deux compacts et . Posons .

Puisque f est continue sur K, alors elle est uniformément continue sur K. Donc:





Si on prend , càd pour tout t dans [0,1], on a |h(t)|< , alors

pour tout t dans [0,1]

C'est équivaut à dire que la fonction converge uniformément vers
lorsque h converge uniformément vers 0.

C'est juste?