Suites

[Theilya]

Bonsoir , je suis bloqué sur cet petit exercice si possible de m'aider

I - On considère les suites définies pour n dans N* par

Un = (1.3.5.....(2n-1)) / (2.4.6.....(2n)) et Vn = (2.4.6....(2n)) / ( 1.3.5....(2n+1) ) et Wn = Un/Vn

1 ) montrer que pour tout n dans N* n/(n+1) < (n+1)/(n+2) . En déduire que 1/4n < Un² < 1/(2n+1)
2 ) montrer que 1/(;)(2n+1)) < Vn < (2;)n)/(2n+1)
3 ) montrer que Wn est une suite décroissante minorée pas 1/2 . On pose dans la suite lim Wn = a
4 ) montrer que Un.Vn ;) (1/(2n)) et Vn ;) (1/(;)a)(;)2n))

j'ai su faire juste la première partie de la première question mais la suite je suis bloqué ...
Merci d'avance

[ilikoko123]

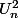
pour la première question essaye d'écrire Un avec un symbole pi , quand tu pose l'expression de le terme dans le symbole se multiplie par lui même , le premier tu le garde et le deuxième tu lui applique une des inégalité que tu viens de démontrer , ça fait apparaitre un produit téléscopique

[Theilya]

merci pour la réponse , je vais éssayer

[Theilya]

j'ai essayé mais le produit télescopique n'apparaît pas

[ilikoko123]

montre moi comment tu trouve Un

[Theilya]

n-1
;) (4k(k+1)+1)/((4k.k).4n²)
k=1

[ilikoko123]

je ne vois pas comment tu as trouvé cette expression
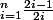
;) n'est ce pas ?

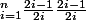
;) n'est ce pas ?

[Theilya]

je ne vois pas comment tu as trouvé cette expression
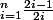
;) n'est ce pas ?

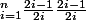
;) n'est ce pas ?

oui j'ai trouvé ça

[ilikoko123]

et alors ?

[Theilya]

pour appliquer l'inégalité au premier terme ça revient à l'appliquer à Un elle même

[ilikoko123]

[Theilya]

ah oui c'est bon , j'ai utilisé la méthode en négligeant le premier terme , Merci beaucoup !