Esapce vectoriel

[bSylvain]

Bonjour à tous,

Je cale sur le sujet ci-dessous,

Soit H l’ensemble des suites (a(n)) n appartient à N à valeurs réelles telles que
;)exp;)(n²) a²(n)<;);)
Démontrer que H est un espace vectoriel réel.

Est ce que vous pourriez m'aide la dessus?

Merci d'avance

[ilikoko123]

le 0 est il dedans ?on prend deux suite dans H , si on les somme ?

[bSylvain]

Les seules informations que j'ai sont celles que j'ai donné.
Pouvez vous m'aider ?

le 0 est il dedans ?on prend deux suite dans H , si on les somme ?

[MouLou]

C'est une question pour toi qu'il posait. Si ce qu'il te demande est vérifié, tu as bien un espace vectoriel , en tant que sous espace vectoriel d'un espace, non? (enfin plutot faudrait combinaison linéaire et pas seulement somme)

[bSylvain]

Oui 0 n prend toutes les valeurs.
Pour moi il faut montrer que la suite est convergente. C est la ou je cale vue la forme de a(n).
Avez vous une idée ?

le 0 est il dedans ?on prend deux suite dans H , si on les somme ?

[SLA]

Oui 0 n prend toutes les valeurs.
Pour moi il faut montrer que la suite est convergente. C est la ou je cale vue la forme de a(n).
Avez vous une idée ?

Tu as l'air un peu perdu.
Tu dois avoir, dans ton cours, une propriété du type " Si E est un espace vectoriel et si H est un sous-espace vectoriel de E, alors H est un espace vectoriel".
La définition de "H est un sous-espace vectoriel de E" est:
-H inclus dans E
-H est non vide
-pour x,y dans H, x+y appartient à H
-pour x dans H et lambda un scalaire, alors lambda . x est dans H.

En pratique, on sait qu'un espace vectoriel possède le vecteur nul. Donc H doit nécessairement posséder ce vecteur nul.

La première chose à faire est de trouver un espace vectoriel E qui contient H. Enfin de montrer que H en est un sous-espace vectoriel. Fais les choses calmement et tout ira bien.
Cordialement

EDIT: J'avais oublié "H inclus dans E"

[MouLou]

"Oui 0 n prend toutes les valeurs."

Je ne comprends pas ce que tu entends par 0 n. 0 c'est la suite définie par

Cette suite vérifie t-elle le critère donné, à savoir ?

Pareil tu prends 2 suites et vérifiant le criètre, et deux réels. La suite vérifie t-elle à son tour le critère?

[bSylvain]

Comme vous dites faisons les choses calmement.

Oui cette suite vérifié le donne car c est l énoncé.


Donc la suite vérifié ce critère le problème est évident !

D après ce que tu as écrit on moontre que c est un espace vectoriel.

Il va falloir que je lise le texte plus tranquillement

Merci à vous

QUOTE=MouLou]"Oui 0 n prend toutes les valeurs."

Je ne comprends pas ce que tu entends par 0 n. 0 c'est la suite définie par

Cette suite vérifie t-elle le critère donné, à savoir ?

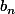Pareil tu prends 2 suites et vérifiant le criètre, et deux réels. La suite vérifie t-elle à son tour le critère?[/quote]

[MouLou]

Effectivement je t'ai donné que la moitié de la démarche. SLA a raison, il faut d'abord trouver un espace vectoriel dont il sera un sous-espace, et la tu verifieras les 3 critères qu'il t'a donné(dont j'ai donné la traduction mathématique dans le post avant)

[SLA]

Par ailleurs, tu auras probablement besoin de l'inégalité suivante (facile à prouver)