Récurrence, étape P(n+1)

[mari5029]

Démontrer , en raisonnant par récurrence , que :

n |N* , 17 divise 3 x 5 puissance (2n-1) + 2puissance (3n-2)

j'ai déjà essayé mais je n'avance pas pour ce qui est de démontrer que P(n+1) est vraie . :hum:

[zygomatique]

salut



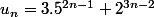
je pose n = n + 1



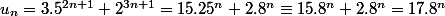
pas besoin de récurrence ... :zen:


avec récurrence ::



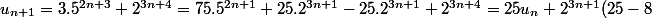or 25 - 8 = 17 a le bon gout d'être multiple de 17 ...

on peut donc récurer ...

:zen:

[bellachia2012]

Démonstration par récurrence que ;) n ;)|N* , 17 divise 3 x 5 puissance (2n-1) + 2puissance (3n-2)
1/ vérifier pour n=1 donc u1 = 3x5 + 2 = 17 donc pour n=1 u1 est divisible par 17.
supposons que elle est vrai pour le rang n càd :
;) n ;)|N* , un = 3 x 5 puissance (2n-1) + 2puissance (3n-2) est divisible par 17
Et vérifiant quelle est vrai pour le rang n+1
u(n+1) divise 17.
Monsieur Zygomatique à bien vérifier pour n =n+1 dans la ligne 2 et 3 que je le remercier.
Donc à la fin après vérification pour n+1, en dit que :
;) n ;)|N* , 17 divise 3 x 5 puissance (2n-1) + 2puissance (3n-2)
Fin du raisonnement par récurrence.

[mari5029]

[quote="zygomatique"]salut



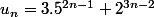
je pose n = n + 1

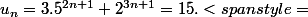
25^n + 2.8^n \equiv 15.8^n + 2.8^n = 17.8^n"/>


je n'ai pas compris ce que j'ai mis en gras :hein:

25^n =/= 8^n

Je vous remercie pour l'explication!

[zygomatique]

ne connais-tu pas la relation de congruence ?

a - b est multiple de n

et 25 = 17 + 8 donc

:lol3:

[bellachia2012]

Un raisonnement par récurrence c'est un raisonnement par récurrence, malgré Votre réponse est juste mais se n'ai pas pas un raisonnement par récurrence Monsieur zygomatique..

[mathelot]

Si P(n+1) est démontré , alors l'hérédité
est vraie.

[zygomatique]

Un raisonnement par récurrence c'est un raisonnement par récurrence, malgré Votre réponse est juste mais se n'ai pas pas un raisonnement par récurrence Monsieur zygomatique..

je t'ai fait deux démonstrations, l'une sans récurrence et l'autre par récurrence ...

:lol3: