Dl

par **adamNIDO** » 03 Nov 2015, 16:27

Bonjour,

je voudrais montrer que

remarquons que

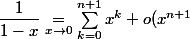dérivons par rapport

:

Donc j'ai trouvé que

varie entre

et

et pas entre $0$ et $n$
Pouvez-vous m'expliquer pourquoi ?
Merci d'avance.

par **Kolis** » 03 Nov 2015, 16:49

Quand tu passes de la ligne ...

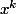
... à ...

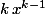
... pourquoi changes-tu la limite de sommation

en

?

par **MouLou** » 03 Nov 2015, 16:50

Salut. A une ligne tu as n+1, à la suivante tu as n.

par **adamNIDO** » 03 Nov 2015, 17:18

salut,

j'ai cru quand dérive une sommation on soustraire un élément de la limite de sommation par exemple n+1 devient n

merci

par **MouLou** » 03 Nov 2015, 18:44

Non, juste le k qui devient k-1 (et donc a fortiori apres changement d'indice, n devient n-1, mais pas les 2 a la fois)