Suites récurrentes linéaires d'ordre 1 - Licence 3 Éco
13 messages
- Page 1 sur 1
Suites récurrentes linéaires d'ordre 1 - Licence 3 Éco
Bonjour à tous,
Cette année je suis un cours (obligatoire) de "Mathématiques des systèmes dynamiques" et je ne comprend absolument rien, mon prof n'étant objectivement pas très pédagogue et mes camarades étant dans le même cas que moi.
Ainsi, je dois rendre la semaine prochaine un DM, qui correspond à l'un des exercices de ma fiche.
Bref si vous pouviez m'aider, vous rendriez service à toute une classe dans le besoin :ptdr:
Je préfère vous mettre le lien directement : ****Merci de recopier l'énnoncé*****
Il s'agit de l'exercice 4.
Si vous pouviez au moins m'indiquer ce qu'il faut faire, si calculs il y a, je peux bien les faire tout seul (enfin je pense) mais je ne sais même pas comment commencer...
Merci d'avance pour vos réponses :lol3:
Cette année je suis un cours (obligatoire) de "Mathématiques des systèmes dynamiques" et je ne comprend absolument rien, mon prof n'étant objectivement pas très pédagogue et mes camarades étant dans le même cas que moi.
Ainsi, je dois rendre la semaine prochaine un DM, qui correspond à l'un des exercices de ma fiche.
Bref si vous pouviez m'aider, vous rendriez service à toute une classe dans le besoin :ptdr:
Je préfère vous mettre le lien directement : ****Merci de recopier l'énnoncé*****
Il s'agit de l'exercice 4.
Si vous pouviez au moins m'indiquer ce qu'il faut faire, si calculs il y a, je peux bien les faire tout seul (enfin je pense) mais je ne sais même pas comment commencer...
Merci d'avance pour vos réponses :lol3:
Thomas94140 a écrit:Bonjour à tous,
Cette année je suis un cours (obligatoire) de "Mathématiques des systèmes dynamiques" et je ne comprend absolument rien, mon prof n'étant objectivement pas très pédagogue et mes camarades étant dans le même cas que moi.
Ainsi, je dois rendre la semaine prochaine un DM, qui correspond à l'un des exercices de ma fiche.
Bref si vous pouviez m'aider, vous rendriez service à toute une classe dans le besoin :ptdr:
Je préfère vous mettre le lien directement : ****Merci de recopier l'énnoncé*****
Il s'agit de l'exercice 4.
Si vous pouviez au moins m'indiquer ce qu'il faut faire, si calculs il y a, je peux bien les faire tout seul (enfin je pense) mais je ne sais même pas comment commencer...
Merci d'avance pour vos réponses :lol3:
Question 1 : un état d'équilibre potentiel, c'est un réel x tel que f(x)=x
(En maths pures (non appliquées), on appelle ça un point fixe de la fonction f)
Question 2 : il faut montrer que f([-3 ; 3]) est inclus dans [-3 ; 3]
chombier a écrit:Question 1 : un état d'équilibre potentiel, c'est un réel x tel que f(x)=x
(En maths pures (non appliquées), on appelle ça un point fixe de la fonction f)
Question 2 : il faut montrer que f([-3 ; 3]) est inclus dans [-3 ; 3]
Déjà merci pour ta réponse.
Je suis vraiment désolé mais j'ai un niveau très très médiocre en maths.
Si je comprends bien, pour la question 1, je dois trouver un réel x tel que f(x) = x et ce réel c'est mon état d'équilibre ? Et comment je fais cela ?
Et pour l'équation récurrente ?
Pour la question 2, comment peut-on montrer cela ?
pour les suites , on a la formule de récurrence
)
la fonction f s'obtient en remplaçant par
par  dans l'expression.
dans l'expression.
Les états stables s'obtiennent en posant l'équation d'inconnue x
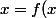)
Une fois déterminée la fonction f , on trace son tableau de variation
ce qui permet de dire si un intervalle I est stable par f ou non
On se pose la question \subset I.) ?
?
si oui la propriété s'étudie par récurrence sur l'entier n.
s'étudie par récurrence sur l'entier n.
A l'exo 4, l'équation aux points fixes est de degré 2 en posant l'inconnue
la fonction f s'obtient en remplaçant
Les états stables s'obtiennent en posant l'équation d'inconnue x
Une fois déterminée la fonction f , on trace son tableau de variation
ce qui permet de dire si un intervalle I est stable par f ou non
On se pose la question
si oui la propriété
A l'exo 4, l'équation aux points fixes est de degré 2 en posant l'inconnue
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
