Réponse en fréquence, filtre.
De la mécanique au nucléaire, nos physiciens sont à l'écoute
-
Etudiant69
- Messages: 4
- Enregistré le: 01 Jan 2015, 07:51
-
 par Etudiant69 » 19 Oct 2015, 01:25
par Etudiant69 » 19 Oct 2015, 01:25
Bonsoir,
Je vous expose mon problème.
J'ai besoin de calculer la fonction de transfert d'un filtre passe-bas d'ordre 2.
Voici la bête:
[img]
[IMG]http://img11.hostingpics.net/pics/47241618fo.png[/img][/IMG]
1/Calcul de la valeur du potentiel Va .Zc1}{2.Zc1+R}) Donc:
Donc: Va(2.Zc1+R)
= Ve.Zc1 + Vs.R + Va.Zc1 - Vs.Zc1
Va(Zc1+R)
= Ve.Zc1 + Vs(R-Zc1)
}{Zc1+R}) 2/ J'applique ensuite un diviseur de tension pour le calcul de Vb
2/ J'applique ensuite un diviseur de tension pour le calcul de Vb  3/ Combinaison des deux équations précédentes
3/ Combinaison des deux équations précédentes }{Zc1+R})
}{(R+Zc2).(Zc1+R)}) Donc:
Donc: Vs(R+Zc2)(Zc1+R)
=Ve.Zc1.Zc2+Vs.Zc2(R-Zc1)
Vs(2R+Zc1+Zc2+Zc2.R+Zc2.Zc1)
= Ve.Zc1.Zc2
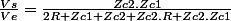
J'essaye ensuite de développer cette expression de façon à avoir une fonction de la forme généralisée d'un système d'ordre 2.
J'ai beau chercher mais impossible de tomber sur un résultat cohérent ...
Alors voilà, mes questions sont simples:
Est-ce une méthode qui fonctionne ? Et si c'est bien le cas, ou sont mes erreurs ? Merci, à tous ceux qui prendront le temps de lire et/ou de répondre.
Bonne nuit.

-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 19 Oct 2015, 08:54
par Pisigma » 19 Oct 2015, 08:54
Etudiant69 a écrit:Bonsoir,
Je vous expose mon problème.
J'ai besoin de calculer la fonction de transfert d'un filtre passe-bas d'ordre 2.
Voici la bête:
[img]
[IMG]http://img11.hostingpics.net/pics/47241618fo.png[/img][/IMG]
1/Calcul de la valeur du potentiel Va .Zc1}{2.Zc1+R}) Donc:
Donc: Va(2.Zc1+R)
= Ve.Zc1 + Vs.R + Va.Zc1 - Vs.Zc1
Va(Zc1+R)
= Ve.Zc1 + Vs(R-Zc1)
}{Zc1+R}) 2/ J'applique ensuite un diviseur de tension pour le calcul de Vb
2/ J'applique ensuite un diviseur de tension pour le calcul de Vb  3/ Combinaison des deux équations précédentes
3/ Combinaison des deux équations précédentes }{Zc1+R})
}{(R+Zc2).(Zc1+R)}) Donc:
Donc: Vs(R+Zc2)(Zc1+R)
=Ve.Zc1.Zc2+Vs.Zc2(R-Zc1)
Vs(2R+Zc1+Zc2+Zc2.R+Zc2.Zc1)
= Ve.Zc1.Zc2
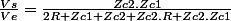
J'essaye ensuite de développer cette expression de façon à avoir une fonction de la forme généralisée d'un système d'ordre 2.
J'ai beau chercher mais impossible de tomber sur un résultat cohérent ...
Alors voilà, mes questions sont simples:
Est-ce une méthode qui fonctionne ? Et si c'est bien le cas, ou sont mes erreurs ? Merci, à tous ceux qui prendront le temps de lire et/ou de répondre.
Bonne nuit.

Bonjour,
Es-tu sur de Va, n'est-ce pas plutôt:
}{2Z_{c1}+R})
Vb me paraît OK
-
Etudiant69
- Messages: 4
- Enregistré le: 01 Jan 2015, 07:51
-
 par Etudiant69 » 19 Oct 2015, 09:38
par Etudiant69 » 19 Oct 2015, 09:38
Pisigma a écrit:Bonjour,
Es-tu sur de Va, n'est-ce pas plutôt:
}{2Z_{c1}+R})
Vb me paraît OK
Bonjour Pisigma,
Je ne comprends toujours pas pourquoi j'ai voulu appliquer cette différence de potentiel (Va-Vs) aux bornes de C1, c'est complètement con, j'avais aussi tenté un Millman. Mettons ça sur le compte de la fatigue :ptdr: .
Ceci dit, merci pour ton aide. J'ai refait l'étude du filtre complet et tout tombe niquel :we: ;
Bonne journée
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 19 Oct 2015, 10:26
par Pisigma » 19 Oct 2015, 10:26
Etudiant69 a écrit:Bonjour Pisigma,
Je ne comprends toujours pas pourquoi j'ai voulu appliquer cette différence de potentiel (Va-Vs) aux bornes de C1, c'est complètement con, j'avais aussi tenté un Millman. Mettons ça sur le compte de la fatigue :ptdr: .
Ceci dit, merci pour ton aide. J'ai refait l'étude du filtre complet et tout tombe niquel :we: ;
Bonne journée
Bonne journée à toi aussi.
Tu reviens quand tu veux :lol3:
-
Black Jack
 par Black Jack » 19 Oct 2015, 14:57
par Black Jack » 19 Oct 2015, 14:57
L'ampli est monté en suiveur --> Vb = Vs
(Vi - Va)/R = jw.C1.(Va - Vs) + (Va - Vs)/R (équation du noeud de potentiel Va)
(Va-Vs)/R = jwC2.Vs
Va = Vs.(1 + jwRC2)
(Vi - Vs.(1 + jwRC2)) = jw.R.C1.(Vs.(1 + jwRC2) - Vs) + (Vs.(1 + jwRC2) - Vs)
Vi - Vs.(1 + jwRC2) = jw.R.C1.(Vs.jwRC2) + Vs.jwRC2
Vi = Vs(1 + 2jwRC2 + j²w².R².C1.C2)
Vs/Vi = 1/(1 + 2jwRC2 + j²w².R².C1.C2)
Calculs non vérifiés. :zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
