Intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
sircroco
- Membre Naturel
- Messages: 18
- Enregistré le: 26 Sep 2015, 12:44
-
 par sircroco » 17 Oct 2015, 17:08
par sircroco » 17 Oct 2015, 17:08
Bonsoir,
comment je peux faire l'intégrale de
xRAC(1-x^4) svp (changement de variable)
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 17 Oct 2015, 17:14
par Pisigma » 17 Oct 2015, 17:14
sircroco a écrit:Bonsoir,
comment je peux faire l'intégrale de
xRAC(1-x^4) svp (changement de variable)
Bonsoir,
pose
)
-
sircroco
- Membre Naturel
- Messages: 18
- Enregistré le: 26 Sep 2015, 12:44
-
 par sircroco » 17 Oct 2015, 17:24
par sircroco » 17 Oct 2015, 17:24
Pisigma a écrit:Bonsoir,
pose
)
ça fait integrale de rac(sin(t)) * rac(sin(t)+1) * sin(t)/cos(t)
ensuite ??

-
WillyCagnes
- Membre Transcendant
- Messages: 3753
- Enregistré le: 21 Sep 2013, 19:58
-
 par WillyCagnes » 17 Oct 2015, 17:40
par WillyCagnes » 17 Oct 2015, 17:40
bjr
Pisigma t'a bien aidé dans le changement de variable
x²=sint
la dérivée donne
2xdx=cos(t) dt
I=integrale(xV(1-x^4)dx
avec le chg de variable cela donne
I=int(1/2*cos(t)V(1-sin²(t))dt)
I=int(1/2 *cos²(t) dt)
or cos²(t)= 1/2 +cos(2t)/2
te laisse faire le calcul de l'integrale
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 17 Oct 2015, 17:46
par Pisigma » 17 Oct 2015, 17:46
sircroco a écrit:ça fait integrale de rac(sin(t)) * rac(sin(t)+1) * sin(t)/cos(t)
ensuite ??

Si tu poses
)
je ne vois pas d'où tu sors ta réponse.
On a
dt)
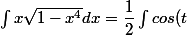\sqrt{1-sin^2(t)}dt)
-
sircroco
- Membre Naturel
- Messages: 18
- Enregistré le: 26 Sep 2015, 12:44
-
 par sircroco » 17 Oct 2015, 18:31
par sircroco » 17 Oct 2015, 18:31
Pisigma a écrit:
Si tu poses
)
je ne vois pas d'où tu sors ta réponse.
On a
dt)
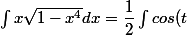\sqrt{1-sin^2(t)}dt)
désolé j'avais jamais fais ce genre de changement de variable, j'ai toujours fais pour l'instant avec des changement interne, par exemple u = x ou 1-x^4, je sais pas si tu comprends.
au final je trouve 1/2*[(1/2)+(1/4*sin(2t))]
est-ce correct ?
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 17 Oct 2015, 18:39
par Pisigma » 17 Oct 2015, 18:39
sircroco a écrit:désolé j'avais jamais fais ce genre de changement de variable, j'ai toujours fais pour l'instant avec des changement interne, par exemple u = x ou 1-x^4, je sais pas si tu comprends.
au final je trouve 1/2*[(1/2)+(1/4*sin(2t))]
est-ce correct ?
1/2*[(1/2)+(1/4
t*sin(2t))]
d'où une primitive en x...
-
sircroco
- Membre Naturel
- Messages: 18
- Enregistré le: 26 Sep 2015, 12:44
-
 par sircroco » 17 Oct 2015, 18:43
par sircroco » 17 Oct 2015, 18:43
Pisigma a écrit:1/2*[(1/2)+(1/4t*sin(2t))]
d'où une primitive en x...
d'où sort le t au dénominateur stp ? j'ai vu sur un site que primitive cos(2t) = 1/2*sin(2t) + k :doh:
-
sircroco
- Membre Naturel
- Messages: 18
- Enregistré le: 26 Sep 2015, 12:44
-
 par sircroco » 17 Oct 2015, 18:45
par sircroco » 17 Oct 2015, 18:45
sircroco a écrit:d'où sort le t au dénominateur stp ? j'ai vu sur un site que primitive cos(2t) = 1/2*sin(2t) + k :doh:
primitive 1/2 + cos(2t)/2 =
(t/2) + (1/4)*sin(2t)
???
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 17 Oct 2015, 19:31
par Pisigma » 17 Oct 2015, 19:31
sircroco a écrit:primitive 1/2 + cos(2t)/2 =
(t/2) + (1/4)*sin(2t)
???
 dt =\dfrac{1}{2}\int\dfrac{1+cos(2t)}{2}dt=\dfrac{1}{2}[\dfrac{t}{2}+\dfrac{sin(2t)}{2}])
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
je ne vois pas d'où tu sors ta réponse.
dt)
