Factorisation
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
visiondudos
- Membre Naturel
- Messages: 22
- Enregistré le: 19 Mai 2015, 08:57
-
 par visiondudos » 16 Oct 2015, 06:29
par visiondudos » 16 Oct 2015, 06:29
Bonjour,
Petit souci avec une factorisation :

edit:
équation de départ ->
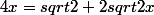
Le souci c'est que dans la solution on me sort :
 = sqrt{2})
Comment peut-on mettre x en facteur alors qu'il est sous racine ?

<-- ??
En vous remerciant d'avance de vos réponses.
-
Grimmys
- Membre Relatif
- Messages: 117
- Enregistré le: 09 Juil 2015, 19:16
-
 par Grimmys » 16 Oct 2015, 06:54
par Grimmys » 16 Oct 2015, 06:54
Salut, effectivement, tu peux utiliser l'égalité suivante :

Après, je ne vois pas comment ils obtiennent ça... C'est chiant les solution non détaillées.
-
visiondudos
- Membre Naturel
- Messages: 22
- Enregistré le: 19 Mai 2015, 08:57
-
 par visiondudos » 16 Oct 2015, 07:24
par visiondudos » 16 Oct 2015, 07:24
Grimmys a écrit:Salut, effectivement, tu peux utiliser l'égalité suivante :

Après, je ne vois pas comment ils obtiennent ça... C'est chiant les solution non détaillées.
Il détaille, mais seulement pour la suite de l'équation x)
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 16 Oct 2015, 07:25
par nodjim » 16 Oct 2015, 07:25
La solution présentée est fausse.
On pose 4x-2=2V(2x)
On met au carré (x>0) et on résout.
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 16 Oct 2015, 08:01
par nodjim » 16 Oct 2015, 08:01
Si on change l'énoncé sans prévenir.....
-
visiondudos
- Membre Naturel
- Messages: 22
- Enregistré le: 19 Mai 2015, 08:57
-
 par visiondudos » 16 Oct 2015, 12:40
par visiondudos » 16 Oct 2015, 12:40
nodjim a écrit:Si on change l'énoncé sans prévenir.....
Sa reste la même chose <__<', j'ai préféré mettre l'équation de départ au cas où..

-
laetidom
- Habitué(e)
- Messages: 5720
- Enregistré le: 16 Déc 2013, 16:15
-
 par laetidom » 16 Oct 2015, 12:52
par laetidom » 16 Oct 2015, 12:52
visiondudos a écrit:Sa reste la même chose <__<', j'ai préféré mettre l'équation de départ au cas où..
Bjr,
c'est-à-dire ? ... <__<' ?...
-
Grimmys
- Membre Relatif
- Messages: 117
- Enregistré le: 09 Juil 2015, 19:16
-
 par Grimmys » 16 Oct 2015, 21:46
par Grimmys » 16 Oct 2015, 21:46
Ah ben d'un seul coup tout va mieux, avant ton édit on avait une expression de départ qui ne coïncidait pas.
Là, on passe simplement le 2*sqrt(2x) à gauche et on peut factoriser en utilisant effectivement l'égalité que je t'ai donné plus haut.
-
visiondudos
- Membre Naturel
- Messages: 22
- Enregistré le: 19 Mai 2015, 08:57
-
 par visiondudos » 17 Oct 2015, 14:49
par visiondudos » 17 Oct 2015, 14:49
Grimmys a écrit:Ah ben d'un seul coup tout va mieux, avant ton édit on avait une expression de départ qui ne coïncidait pas.
Là, on passe simplement le 2*sqrt(2x) à gauche et on peut factoriser en utilisant effectivement l'égalité que je t'ai donné plus haut.
Je suis carrément perdu, comment peut-on factoriser de :
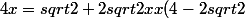 = sqrt{2})
?
même avec l'égalité, je ne peux pas factoriser un x avec une racine de x.
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 17 Oct 2015, 17:24
par Carpate » 17 Oct 2015, 17:24
visiondudos a écrit:Je suis carrément perdu, comment peut-on factoriser de :
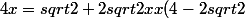 = sqrt{2})
?
même avec l'égalité, je ne peux pas factoriser un x avec une racine de x.
Ben oui, personne ne pourrait factoriser ainsi !
-
MABYA
- Membre Relatif
- Messages: 401
- Enregistré le: 13 Mar 2015, 14:37
-
 par MABYA » 17 Oct 2015, 17:26
par MABYA » 17 Oct 2015, 17:26
ton égalité 4xx=V2+2V(2x) = x(4-2V2)=V2 est fausse
c'est V(2x) et non 2xV2
La solution qui me paraît envisageable c'est d'isoler 2V(2x) puis élever les deux membres au carré
Tu vas tomber sur une équation du second degré, il y aura des V2 mais les Vx auront disparu,
parce que (2V(2x))²=4(2x) = 8x
en priant un de tes dieux pour que cette équation ait des racines tu pourras mettre sous la forme a(x-x')(x-x") et tu auras factorisé
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités