Décomposer en élément simple
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
master500
- Membre Naturel
- Messages: 48
- Enregistré le: 16 Mai 2010, 17:14
-
 par master500 » 06 Oct 2015, 22:30
par master500 » 06 Oct 2015, 22:30
Bonjour je viens vers vous pour vous demander de m'éclaircir sur un point :
F =
(X^2+1)})
la question est : décomposer F en élément simple.
J'ai donc chercher avec les identités remarquable etc mais ça ne donne rien, cependant j'ai la correction qui me dit.
deg(F) = 0-(2+2) = -4
mais je ne comprend rien du tout, ou de comment partir car en ce moment nous sommes sur les complexes et sincèrement je n'est jamais vu ce deg(F) = ...
Merci d'avance si quelqu'un aurait une méthode plus simple je suis également preneur.
-
danyL
- Membre Rationnel
- Messages: 682
- Enregistré le: 03 Jan 2015, 13:29
-
 par danyL » 07 Oct 2015, 00:11
par danyL » 07 Oct 2015, 00:11
master500 a écrit:Bonjour je viens vers vous pour vous demander de m'éclaircir sur un point :
F =
(X^2+1)})
la question est : décomposer F en élément simple.
J'ai donc chercher avec les identités remarquable etc mais ça ne donne rien, cependant j'ai la correction qui me dit.
mais je ne comprend rien du tout, ou de comment partir car en ce moment nous sommes sur les complexes et sincèrement je n'est jamais vu ce deg(F) = ...
Merci d'avance si quelqu'un aurait une méthode plus simple je suis également preneur.
bonjour ou bonsoir
tu connais "une équation du second
degré " : a x² + bx + c
trinome avec le plus haut degré de x = 2
ici pas de x au numérateur -> degré 0
au dénominateur : terme de plus haut degré 2 multiplié par terme de plus haut degré 2 -> degré 4

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 07 Oct 2015, 06:47
par chan79 » 07 Oct 2015, 06:47
salut
tu as dû voir en cours qu'il existe 4 nombres complexes a, b, c et d tels que

-
master500
- Membre Naturel
- Messages: 48
- Enregistré le: 16 Mai 2010, 17:14
-
 par master500 » 07 Oct 2015, 16:19
par master500 » 07 Oct 2015, 16:19
D'accord je cherche tout ça ce soir et je posterai mes avancés demain, merci à vous en tout cas

-
WillyCagnes
- Membre Transcendant
- Messages: 3753
- Enregistré le: 21 Sep 2013, 19:58
-
 par WillyCagnes » 07 Oct 2015, 16:51
par WillyCagnes » 07 Oct 2015, 16:51
bsr,
F(x) =1/[2(x²-1)] -1/[2(x²+1)]
x²-1=(x+1)(x-1)
or 1/[2(x²-1)] =1/[4(x+1)] -1/[4(x²+1)]

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 07 Oct 2015, 16:59
par chan79 » 07 Oct 2015, 16:59
WillyCagnes a écrit:
or 1/[2(x²-1)] =1/[4(x+1)] -1/[4(x²+1)]
ça n'a pas l'air de coller pour x=0
Tu as:
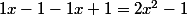
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
