L'implication =>
26 messages
- Page 1 sur 2 - 1, 2
zygomatique a écrit:une définition ne se comprend pas elle s'apprend ....
Une définition logique se justifie avec la table de vérité associée : http://exo7.emath.fr/cours/ch_logique.pdf
oui et non ...en fait plutôt non (en ce qui me concerne j'appelle pas ça une definition)
l'implication est faite selon
0=>0 =1
0=>1 =1
1=> 0 =0
1=>1=1
or il se trouve que l'ensemble des lois de composition internes que l'on peut munir dans l'ensemble {0,1}
peut se traduire avec le non logique et la loi + (ou non exclusif) et la loi . (ET)
et on voit tres bien que
x=> y est equivallent à : NON(x)+y
l'implication est faite selon
0=>0 =1
0=>1 =1
1=> 0 =0
1=>1=1
or il se trouve que l'ensemble des lois de composition internes que l'on peut munir dans l'ensemble {0,1}
peut se traduire avec le non logique et la loi + (ou non exclusif) et la loi . (ET)
et on voit tres bien que
x=> y est equivallent à : NON(x)+y
il s'en fiche il veut savoir pourquoi
x=>y c'est kif kif identique à NON(x) (+OU NON EXCLUSIF) y
eh bien ça c'est pas la definition qui le decrete
mais ça ->
x=>y c'est kif kif identique à NON(x) (+OU NON EXCLUSIF) y
eh bien ça c'est pas la definition qui le decrete
mais ça ->
alphamethyste a écrit:oui et non ...en fait plutôt non (en ce qui me concerne j'appelle pas ça une definition)
l'implication est faite selon
0=>0 =1
0=>1 =1
1=> 0 =0
1=>1=1
or il se trouve que l'ensemble des lois de composition internes que l'on peut munir dans l'ensemble {0,1}
peut se traduire avec le non logique et la loi + (ou non exclusif) et la loi . (ET)
et on voit tres bien que
x=> y est equivallent à : NON(x)+y
Je déteste lorsque l'on dis "y'a rien à comprendre il faut apprendre".
On peut effectivement définir l'implication "A => B" comme "B ou non(A)".
En effet on dira qu'une implication est vraie soit si la conclusion est vraie, soit si le point de départ est faux.
C'est un peu surprenant au premier regard car cela signifie que
" 1=2 => e^2 B soit vraie.
Alors si on montre que A est vraie on sait que B est vraie.
En revanche si on montre que B est vraie on ne sait rien sur A :zen:
Si A = > B n'est pas vraie on ne peut pas dire grand chose du tout...
(sauf que A et B ne peuvent pas être vraie en même temps).
On peut effectivement définir l'implication "A => B" comme "B ou non(A)".
En effet on dira qu'une implication est vraie soit si la conclusion est vraie, soit si le point de départ est faux.
C'est un peu surprenant au premier regard car cela signifie que
" 1=2 => e^2 B soit vraie.
Alors si on montre que A est vraie on sait que B est vraie.
En revanche si on montre que B est vraie on ne sait rien sur A :zen:
Si A = > B n'est pas vraie on ne peut pas dire grand chose du tout...
(sauf que A et B ne peuvent pas être vraie en même temps).
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Je déteste lorsque l'on dis "y'a rien à comprendre il faut apprendre".
On peut effectivement définir l'implication "A => B" comme "B ou non(A)".
tout est dit !!!!
et comme par hasard les deux objets non a ou b et a => b ont même table de vérité .... comme le hasard mathématique fait bien les choses ....
mais comme le dit Sylviel rien n'interdit de comprendre de quoi l'on parle ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
La plupart des gens seront d'accord pour dire que falsifier "Si A, alors B", c'est trouver une instance où on a A mais pas B, c.-à-d. où "A et (non B)" est vérifié. Et la négation de "A et (non B)", c'est ...
Remarque pour embrouiller tout le monde : en logique intuitionniste,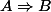 n'est pas équivalent à (non A) ou B. On a seulement l'implication "(non A) ou B" entraîne
n'est pas équivalent à (non A) ou B. On a seulement l'implication "(non A) ou B" entraîne 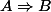 .
.
Remarque pour embrouiller tout le monde : en logique intuitionniste,
Robot a écrit:La plupart des gens seront d'accord pour dire que falsifier "Si A, alors B", c'est trouver une instance où on a A mais pas B, c.-à-d. où "A et (non B)" est vérifié. Et la négation de "A et (non B)", c'est ...
Je trouve cette façon de présenter les choses très intuitive :+:
En ce qui me concerne je trouve plus facile de me représenter mentalement les choses ainsi (peut-être est-il plus facile de raisonner avec des ET que des OU, ne serait-ce qu'à cause du caractère exclusif du OU qu'on rencontre dans la vie de tous les jours ?)
Ensuite, bien sûr il n'y a qu'à faire confiance à monsieur De Morgan...
soit A noté A+ quand réalisé et A- quand non réalisé
idem B
alors on a:
A+A+A-A+A-A-A+
B+B+B+B+B-B-B+
si A vrai alors B vrai
si A faux alors B vrai quand B vrai et si A faux B faux quand B faux
admettons par exemple 2/3 de B+ sur les A- et 1/3 de B- sur les A-
que dois-je penser?:
1) la logique des assertions ne s'applique pas car il ne s'agit pas d'assertion????
donc exit les tables de vérité?
2)si A alors B reste vrai quand A faux????
3) mais non c'est encore autre chose
idem B
alors on a:
A+A+A-A+A-A-A+
B+B+B+B+B-B-B+
si A vrai alors B vrai
si A faux alors B vrai quand B vrai et si A faux B faux quand B faux
admettons par exemple 2/3 de B+ sur les A- et 1/3 de B- sur les A-
que dois-je penser?:
1) la logique des assertions ne s'applique pas car il ne s'agit pas d'assertion????
donc exit les tables de vérité?
2)si A alors B reste vrai quand A faux????
3) mais non c'est encore autre chose
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Robot a écrit:Beagle, je n'arrive pas à trouver du sens à ce que tu écris.
j'ai une série d'évènements , l'un A l'autre B
quand A j'aurais toujours B
donc A vrai implique B vrai
quand A faux j'ai 2/3 de B vrai et 1/3 de B faux
que signifie "A faux implique B" est vrai?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
dans ton cas "A faux implique B vrai" est faux puisque tu peux trouver un A faux et un B faux en même temps.
Exemple :
A : x= 2
B : x^2 = 4
Quand tu as A, tu as B on est bien d'accord
Quand tu n'as pas A, des fois tu n'as pas B (par exemple si x = 1)
et des fois tu l'as (si x = -2).
On est bien dans le cas que tu proposes.
Quand x = 1 on a bien A et B faux en même temps.
Par contre, ce que tu peux dire, c'est que B faux implique A faux (contraposée)
Désolé si je ne suis pas clair , mais j'ai également du mal à comprendre ta question précise...
Exemple :
A : x= 2
B : x^2 = 4
Quand tu as A, tu as B on est bien d'accord
Quand tu n'as pas A, des fois tu n'as pas B (par exemple si x = 1)
et des fois tu l'as (si x = -2).
On est bien dans le cas que tu proposes.
Quand x = 1 on a bien A et B faux en même temps.
Par contre, ce que tu peux dire, c'est que B faux implique A faux (contraposée)
Désolé si je ne suis pas clair , mais j'ai également du mal à comprendre ta question précise...
Robot a écrit:Toujours pas de sens dans ce que tu écris.
J'essaie de donner un sens.
Tu te demandes si l'assertion "(non A) implique B" est vraie (là, j'interprète ce que tu écris de façon à ce que ça fasse sens).
Elle est vraie si A est faux et B est vrai.
Elle est fausse si A est faux et B est faux.
argh, je croyais que dans p implique q
si p est faux, p implique q toujours vrai
ce que je traduissais par si A faux alors peu importe le résultat de B,
A faux implique B est vrai
sauf que je ne comprends pas ce que cela voulait dire...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
désolé il manque des virgules
dans ton cas "A faux implique B vrai" est faux puisque tu peux trouver un A faux et un B faux en même temps.
je parle de
A faux implique B
cette implication est vraie quel que soit B , vrai ou faux
C'est juste que "A faux implique B" vrai, je ne vois pas ce que cela signifie , ce que cela dit, ce que cela raconte ...
dans ton cas "A faux implique B vrai" est faux puisque tu peux trouver un A faux et un B faux en même temps.
je parle de
A faux implique B
cette implication est vraie quel que soit B , vrai ou faux
C'est juste que "A faux implique B" vrai, je ne vois pas ce que cela signifie , ce que cela dit, ce que cela raconte ...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
26 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
