Limites de fonctions

[pinkfloyder]

Bonjour à tous,
j'ai un dm pour jeudi et et jsuis bloqué au dernier exo encore une fois !

Soit f la fonction définie sur R \ {0} par f(x) = x racine de 1+ 1/x²
et Cf sa courbe dans un repère orthonormal o,i,j

1) Demontrer que f est impaire
On appelle g la restriction de f à l'intervalle I = ]0;+ infini[
et Cg sa courbe représentative dans le repère précedent.

2)Déterminer les limites de g en 0 et + infini

3) Démontrer que g est croissante sur I

4) On pose h(x) = g(x) - x
Déterminer la limite de h en + infini et interpréter graphiquement le résultat

5) Déterminer lim quand x-->0 de (g(x)-1)/x

Mes réponses :

1) f(-x) = -x racine de 1-(1/x²) = -f(x) donc impaire
2)lim f(x) en 0 --> pas trouvé
lim f(x) en + infini = + infini

le reste je suis bloqué

merci de m'aider !!

[smaths]

Bonsoir,

f(-x) = -x racine de 1-(1/x²) = -f(x) donc impaire

Avant de calculer l'image de -x par f il faut démontrer que Df (Domaine de f)
est symétrique par rapport à zéro.
équivaut à équivaut à 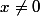équivaut à .
Donc Df est symétrique par rapport à 0.
De plus

2)Déterminer les limites de g en 0 et + infini

Conseil : écrire les termes sous la racine au même dénominateur.

Même conseil pour la limite en l'infini.

3) Démontrer que g est croissante sur I

Penser à la composition de fonction croissante.
et

[pinkfloyder]

Hello,

merci de tes conseils, le 1 et le 2 sont terminés, par contre la dérivée me pose problême.
je sais dériver 1/x² mais avec la racine je ne sais pas .
merci de ton aide