Démonstration de a^-n=1/a^n
22 messages
- Page 1 sur 2 - 1, 2
Démonstration de a^-n=1/a^n
Hey, quelqu'un peut démontrer a^-n=1/a^n
Je trouve rien sur internet.merci.
Je trouve rien sur internet.merci.
[quote="zygomatique"]:cry:
je remplace donc x par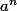 et j'obtiens
et j'obtiens 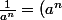^{-1} = a^{-n})
:zen:
PS : les autre démonstrations n'utilisent pas la définition de base ===> qu'elle est-elle cette définition de base, serait-ce x. = 1 ????[/QUOTE]
= 1 ????[/QUOTE]
Ok, bien vu.
---------------------
Juste une précision,
x. = 1 à quoi sert de dire cela pour dire ensuite que l'on pose la relation qui suit (etant donné que c'est celle que l'on cherche à démontrer, c'est ça que je ne comprends pas, excusez-moi de ne pas percuter !)
= 1 à quoi sert de dire cela pour dire ensuite que l'on pose la relation qui suit (etant donné que c'est celle que l'on cherche à démontrer, c'est ça que je ne comprends pas, excusez-moi de ne pas percuter !)
on pose alors (1/x) = x^-1
il suffit alors de remplacer x par a^n
----------------------------------------------
j'ai fait x. = 1
= 1
a^n. = 1
= 1
mais après ça donne a^n = a^n ..... je suis un peu perdu dans cette démo, désolé....
je remplace donc x par
:zen:
PS : les autre démonstrations n'utilisent pas la définition de base ===> qu'elle est-elle cette définition de base, serait-ce x.
Ok, bien vu.
---------------------
Juste une précision,
x.
on pose alors (1/x) = x^-1
il suffit alors de remplacer x par a^n
----------------------------------------------
j'ai fait x.
a^n.
mais après ça donne a^n = a^n ..... je suis un peu perdu dans cette démo, désolé....
il faut revenir à l'ordre des apprentissages !!!
on connaît évidemment la notation fractionnaire !!! (et les opérations avec des fractions ... qui sont apprises avant les exposants)
et donc que l'inverse de x est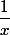
alors une fois qu'on décide par convention de noter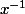 le nombre
le nombre 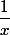
c'est une trivialité de montrer ce qui est demandé ... puisque ce n'est qu'une substitution de symboles : x par a^n
et ça reste alors cohérent avec les règles sur les exposants positifs
on connaît évidemment la notation fractionnaire !!! (et les opérations avec des fractions ... qui sont apprises avant les exposants)
et donc que l'inverse de x est
alors une fois qu'on décide par convention de noter
c'est une trivialité de montrer ce qui est demandé ... puisque ce n'est qu'une substitution de symboles : x par a^n
et ça reste alors cohérent avec les règles sur les exposants positifs
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
paquito a écrit:Comment on fait dans une petite classe pour montrer que, parce il faut déjà commencer par ça!
On admet que tout produit vide vaut 1???
Enfin, si l'on pose, c'est une notation qui ne pourra être justifiée que plus tard!
Dans les petites classes on ne démontre pas que a^0=1. C'est une convention.
On fait quand même remarquer que c'est une convention qui "marche" bien !
Car par exemple x^5/x^3 = (x*x*x*x*x)/(x*x*x) = x^2
Ce qu'on généralise assez facilement pour n différent de m par x^n/x^m = x^(n-m)
En posant x^0=1 la propriété reste vraie pour n=m
titine a écrit:Dans les petites classes on ne démontre pas que a^0=1. C'est une convention.
On fait quand même remarquer que c'est une convention qui "marche" bien !
Car par exemple x^5/x^3 = (x*x*x*x*x)/(x*x*x) = x^2
Ce qu'on généralise assez facilement pour n différent de m par x^n/x^m = x^(n-m)
En posant x^0=1 la propriété reste vraie pour n=m
Cette convention laisse perplexe les élèves; de toute façon, rien n'est démontrable avant le niveau TS
22 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
