Produit matriciel et base canonique

[PCTroyes]

lien du problème

Bonsoir,

Je dois démontrer la proposition 2 du lien ci dessus,
J'ai donc trouvé ce lien, cependant j'ai clairement du mal à comprendre les deltas.
Si quelqu'un peut essayer de me l'expliquer je serai très reconnaissant !

Merci d'avance !

[Yayaj]

Ce sont les symbole de Kronecker : =1 si i=j et 0 sinon

[alphamethyste]

slt (au fait félicitation pour ton pdf il est tres bien: il est tres important voire vital )

tu as la demonstration mais tu voudrai la comprendre alors je change le nom des indices

tu veux demontrer que

on va noter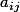 les composantes de la matrice carrée d'ordre n ,


on va noter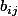 les composantes de la matrice carrée d'ordre n,

on va noter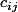 les composantes de la matrice carrée d'ordre n ,

on va noter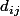 les composantes de la matrice carrée d'ordre n ,

on va noter les composantes de la matrice carrée d'ordre n ,

______________________________

on demontre en deux fois

le cas ci dessous cas d=b=c donc

______________________________

la composante


tandis que toute autre composante de cette matrice est nulle

______________________________

la composante

tandis que toute autre composante de cette matrice est nulle

________________________________________


et étant donné que

la composante

tandis que toute autre composante de cette matrice est nulle

par conséquent les matrices et sont identiques

___________________________________

le cas ci dessous cas et

______________________________

la composante

effectivement car et donc et donc

et donc et donc

la matrice est nulle

______________________________

la composante

tandis que toute autre composante de cette matrice est nulle

________________________________________


et étant donné que

la composante

et en fait la matrice est nulle

par conséquent les matrices et sont identiques

[PCTroyes]

Merci énormément !!!!!!!!!!!!! :++: :ptdr:
Merci pour cette explication très claire et très détaillée !
Ainsi que pour votre temps