Bonjour à toutes et à tous,
Je n'arrive pas a faire un exercice...
Soit un la suite définie par u0=2 et un+1=2un-1
Je dois calculer les premiers termes de la suite et conjecturer la forme explicite de un en fonction de n. Mais je ne comprends pas qu'elle conjecture je dois faire...
Sachant que les premiers termes font 2,3,5,9,17...
Merci d'avance pour vos réponses!
Raisonnement par récurrence
9 messages
- Page 1 sur 1
Salut !
Remarque que :
- pour passer de à
à  , on ajoute
, on ajoute  ;
;
- pour passer de à
à  , on ajoute
, on ajoute  ;
;
- pour passer de à
à  , on ajoute
, on ajoute 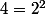 ;
;
- pour passer de à
à 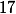 , on ajoute
, on ajoute 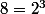 .
.
:we:
Remarque que :
- pour passer de
- pour passer de
- pour passer de
- pour passer de
:we:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Elsapseudo a écrit:Le problème c'est que le terme qui est apres 17 est égal a 33... Or si je fais 17+2^3 ca me fait 25...
C'est toujours la même idée :
- pour passer de
Tu ne vois pas qu'à chaque fois qu'on passe de
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:C'est toujours la même idée :
- pour passer deà
, on ajoute
.
Tu ne vois pas qu'à chaque fois qu'on passe deà
, on ajoute
?
Si si bien sur j'ai vu je me suis trompée apres mais ca mzrche bien! Mais je ne comprends pas comment on conjecture la forme explicite de un en fonction de n!
Ben essaye de remonter les calculs si tu ne le voies pas directement :
 ;
;
 ;
;
 ;
;
 ;
;
...
...
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
