Espace vectoriel

par **nicolas2** » 23 Sep 2015, 19:01

Bonsoir,

J'ai un petit doute sur un exercice.
Soit A(M) et B(M) deux sous-espace vectoriel de M3(R) : M appartient à M3(R) tel que pour A(M) M=MA et pour B(M) AMA=AM
Je dois montrer que A(M) est inclus dans B(M). Ca semble logique, mais je ne sais pas trop comment précéder pour être rigoureux. Je pensais calculer vect(A(M)) et vect(B(M)) puis exprimer vect(A(M)) en fonction de vect(B(M)) mais je ne suis pas sur que cela prouver l'inclusion ni que cela soit la méthode la plus rapide.

Une idée ?
Merci d'avance

par **nicolas2** » 23 Sep 2015, 19:03

Petite correction, ce n'est pas A(M) et B(M) mais A(A) et B(A) bien sur ...

par **Robot** » 23 Sep 2015, 19:23

Ton énoncé est très mal formulé. En plus, l'emploi de deux lettres A désignant deux choses différentes est clamiteux !
Remarque :

est déjà un sous-espace vectoriel de

. Donc prendre

est vraiment une idée farfelue !

par **nicolas2** » 23 Sep 2015, 19:27

Comment montrer l'inclusion alors ?

par **Robot** » 23 Sep 2015, 19:39

En montrant qu'une matrice M qui est dans le premier espace est dans le second. Il suffit de réécrire les définitions des eux espaces, ça vient tout seul

par **nicolas2** » 23 Sep 2015, 19:44

Donc si je prends M la matrice nulle (appartenant à M3(R)), je montre qu'elle appartient au premier espace puis qu'elle appartient au second, cela me prouve l'inclusion ? ..

par **Robot** » 23 Sep 2015, 19:54

Bon, je précise ma quantification : montre que toute matrice M dans le premier espace appartient aussi au second.

par **nicolas2** » 23 Sep 2015, 19:57

Ma question est justement de savoir comment montrer cela en étant le plus rigoureux possible

par **Robot** » 23 Sep 2015, 20:52

En utilisant les définitions des deux espaces. Vas-y au lieu de tourner autour du pot !

par **nicolas2** » 23 Sep 2015, 22:03

Ha c'est moi qui tourne autour du pot ? ...
Je ne sais pas comment faire, si je savais je ne serais pas venu ici.

Je ne demande pas qu'on m'apporte la réponse sur un plateau, simplement m'expliquer la méthode. Comment puis-je montrer que toute matrice M de du premier espace est dans le second ?

par **Robot** » 23 Sep 2015, 22:18

nicolas2 a écrit:Ha c'est moi qui tourne autour du pot ? ...
Je ne sais pas comment faire, si je savais je ne serais pas venu ici.

Je ne demande pas qu'on m'apporte la réponse sur un plateau, simplement m'expliquer la méthode. Comment puis-je montrer que toute matrice M de du premier espace est dans le second ?

J'ai beau t'expliquer la méthode, tu ne bouges pas d'un pouce pour l'appliquer.

Soir

une matrice de

. Par définition de ce sous-espace, on a

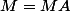
. Par conséquent ... . Donc

appartient à

.
On a montré que

.

Tu n'as plus qu'à remplir les pointillés !

par **nicolas2** » 24 Sep 2015, 06:09

Par conséquent AM=AMA (en multipliant par A des deux cotés), ainsi toute matrice M de A(A) est dans B(A), on retrouve les condition de B(A) en multipliant par A donc A(A) inclus dans B(A)
Ca marche ?

Espace vectoriel

Espace vectoriel

Qui est en ligne