Bonsoir,je suis en premiére Stl et j'ai devoir maison dont je n'ai rien compris,mais qui a l'air assez simple.
Le voici:Écrire la démonstration de l'unicité du nombre neutre pour x et celle de l'unicité de l'inverse.
Aidez-moi s'il cous plait c'est poir demain;);););)
Devoir maison math
8 messages
- Page 1 sur 1
Tu veux démontrer l'unicité de l'élément neutre pour la multiplication dans quel groupe ? 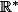 ?
?
Raisonne par l'absurde : suppose qu'il y en a deux et montre qu'en fait ils sont égaux et ce, en utilisant seulement la définition d'un élément neutre.
Raisonne par l'absurde : suppose qu'il y en a deux et montre qu'en fait ils sont égaux et ce, en utilisant seulement la définition d'un élément neutre.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Diviser quoi par 1 ?
Il va falloir être plus clair dans ce que tu dis.
A quel chapitre cet exo correspond-il ?
C'est quoi pour toi le "nombre neutre pour x" ?
je présume qu'on travaille dans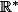 , oui ?
, oui ?
Il va falloir être plus clair dans ce que tu dis.
A quel chapitre cet exo correspond-il ?
C'est quoi pour toi le "nombre neutre pour x" ?
je présume qu'on travaille dans
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
"axiomatique".
'y a pas de soucis.
L'élément neutre dans
dans 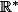 pour la loi
pour la loi  vérifie (par définition) :
vérifie (par définition) :
[CENTER](1) Quel que soit dans
dans 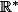 ,
, 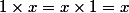 .[/CENTER]
.[/CENTER]
Suppose donc qu'il existe un second élément neutre et notons-le .
.
Dans ce cas, vérifie aussi :
vérifie aussi :
[CENTER](2) Quel que soit dans
dans 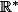 ,
,  .[/CENTER]
.[/CENTER]
Essaye alors de te servir des points (1) et (2) pour montrer qu'en fait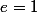 .
.
'y a pas de soucis.
L'élément neutre
[CENTER](1) Quel que soit
Suppose donc qu'il existe un second élément neutre et notons-le
Dans ce cas,
[CENTER](2) Quel que soit
Essaye alors de te servir des points (1) et (2) pour montrer qu'en fait
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
