Determination de z (Niveau L1)

[Yoyo.f]

Bonjour à vous , voilà mon problème
"Déterminer les nombres complexes z tels que z²+2z(barre) - 2 est imaginaire pur " j'ai fais un système d'équation qui est
z=a+ib avec a,b appartenant à R

a²-b²+2a-2=0 --> a²-b²+2a=2
2ib(a-1)=yi -->2b(a-1)=y
Et après je ne vois pas ... et je suis certain qu'il y a une petite astuce

Merci d'avance !! :we:

[lionel52]

La première égalité suffit !
Si a²-b²+2a=2 alors ton complexe est imaginaire pur

Essaie de traduire géométriquement cette égalité

[Yoyo.f]

Il faut que je détermine a et b , il me fait donc au moins deux équations( si je ne pose pas de paramètres) donc la première ne suffit pas .

[lionel52]

Ou alors le problème peut avoir plus qu'une solution, c'est aussi possible

"Déterminer les nombres complexes"

[Yoyo.f]

Il peut y avoir 0 solutions comme une infinité ....

[Robot]

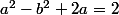
équivaut à . Ca peut faire penser à une courbe assez connue. Mais peut-être ne la connaît-on pas en L1.

[Yoyo.f]

Je ne connais pas cette courbe .

[Robot]

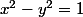
Si ne t'évoque rien, c'est rapé. Mais alors je ne vois pas trop l'intérêt de l'exercice.