Action de groupe

[Trident]

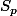
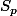
Bonjour à tous. J'ai un petit problème de calcul, je ne vois pas où j'ai fais mon erreur. Soient E et F des A modules (où A est un anneau commutatif). Soit p un entier naturel non nul et on note L_p(E,F) l'ensemble des applications A-linéaires de E^p dans F. On note le groupe symétrique d'ordre p et on veut montrer que l'application suivante définit une action de groupe de sur :


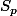
où pour tout dans et dansest l'application qui à associe

Il faut montrer en particulier que pour toutes permutations et , on a
Mais moi je trouve :hum:

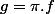
Je note , alors .

Ensuite, l'application associe à tout . C'est donc l'image de par . C'est donc d'après la définition de g plus haut. Et donc c'est l'application .

Où est l'erreur ? Merci.

[Robot]

Ton erreur est ici :

C'est donc l'image de par . C'est donc d'après la définition de g plus haut.

Soit l'ensemble . Je note l'application . Alors

Utilise ce formalisme, tu y verras plus clair.

[Trident]

Ah oui, j'ai compris mon erreur, merci.

[Robot]

Avec plaisir.