Myrtille20 a écrit:Remarque : N'y aurait-il pas une proposition Pn à demontrer pour repondre aux questions 2 et 3 ?
c'est ça la clé
une démonstration par récurrence de cette propriété là que j'ai énoncée
et qui permet de répondre à la question 2 (qui n'est pas faisable à la calculette)
la question 1 est en fait la partie "initialisation" de la démonstration par récurrence.
le problème ouvert est d'énoncer cette propriété Pn (obtenue par conjecture en "observant" les résultats de la question 1)
puis la démonter par récurrence
supposons que ce soit vrai au rang n que
^2 = (33...34)^2)
avec n chiffres 3 soit formé de ces chiffres là (n+1 chiffres 1, puis n chiffres 5 et un chiffre 6)
cela s'écrit aussi avec des puissances de 10 et des formules
(à déterminer : n chiffres 3 ça s'écrit 3 fois le nombre formé par n chiffres 1, qui est lui même
/9)
etc )
si j'ajoute un n+1 ème chiffre 3 devant

qui contient n+1 chiffres (n chiffres 3 et un 4 à la fin), cela s'écrit

développer le carré de
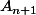
et utiliser l'hypothèse de récurrence
etc ...
une fois cette démonstration effectuée, les questions 2 et 3 se résolvent instantanément avec cette fameuse propriété.
autre méthode : développer la multiplication posée de 333...34²
en traçant précisément toutes les retenues qui se produisent et où
(faire la question 1 totalement sans calculette, en posant la multiplication "école primaire" à la main, peut donner des idées sur ces retenues)
mais cette méthode est moins "mathématique" dans le cadre d'un exercice où on parle d'une propriété Pn, ce qui suggère effectivement une démonstration par récurrence
