Exercice limites de fonctions

[Arca13]

Bonjour, j'ai un exercice de maths (énoncé ci dessous) à faire, je l'ai fait mais le problème est que pour les deux calculs je trouve des formes indéterminables, pouvez-vous me dire si c'est normal ou si je me suis trompé... ? Merci d'avance !

F(x)= (6x²-3x+1) / (x²-2)

Calculer la limite de f en + l'infini
Calculer la limite de f en - l'infini

[lulu math discovering]

Qu'Est-ce que tu trouves ?

[Arca13]

Qu'Est-ce que tu trouves ?

Apres avoir factorisé par le terme de plus haut degrè, je trouve à la fin du +l'infini divisé par du +l'infini du coup c'est pas bon...

[lulu math discovering]

Ok.
Alors, n'ayant pas encore fait ce genre d'exercices, je ne suis pas sur que ma méthode soit très correcte mais bon.

D'abord le dénominateur : lorsque que x devient très grand, le -2 devient négligeable, alors on l'enlève.
Idem pour le numérateur, le 6x² croit beaucoup plus vite que le -3x+1.

Alors on retient 6x²/x² soit 6, et selon le graphique c'est juste.

[Arca13]

Ok.
Alors, n'ayant pas encore fait ce genre d'exercices, je ne suis pas sur que ma méthode soit très correcte mais bon.

D'abord le dénominateur : lorsque que x devient très grand, le -2 devient négligeable, alors on l'enlève.
Idem pour le numérateur, le 6x² croit beaucoup plus vite que le -3x+1.

Alors on retient 6x²/x² soit 6, et selon le graphique c'est juste.

Alors je ne connais pas ta méthode, mon prof ne m'en a pas encore parlé ....

[Carpate]

Apres avoir factorisé par le terme de plus haut degrè, je trouve à la fin du +l'infini divisé par du +l'infini du coup c'est pas bon...

Et si tu simplifiais par ?

[lulu math discovering]

Je ne pense pas que ce soient des maths très propres, c'est plutôt une façon de conjecturer très vite la limite des expressions assez compliquées (un peu comme ici).

C'est une petite technique que je te propose puisque tu avais l'air un peu perdu, et puis ça aide un peu je trouve à saisir le concept de limite.

Sinon, je ne pense pas connaître la vraie solution.

PS : pourquoi fais tu ça carpate ?

[Arca13]

Je ne pense pas que ce soient des maths très propres, c'est plutôt une façon de conjecturer très vite la limite des expressions assez compliquées (un peu comme ici).

C'est une petite technique que je te propose puisque tu avais l'air un peu perdu, et puis ça aide un peu je trouve à saisir le concept de limite.

Sinon, je ne pense pas connaître la vraie solution.

PS : pourquoi fais tu ça carpate ?

Merci de vos réponses ! J'ai pas trop compris la leçon sur les limites du coup j'ai tendance à juste appliquer ce qu'a fait ma prof sur d'autres exemples donc je pense que je vais attendre la correction et je la mettrai sur le forum.

[Carpate]

Merci de vos réponses ! J'ai pas trop compris la leçon sur les limites du coup j'ai tendance à juste appliquer ce qu'a fait ma prof sur d'autres exemples donc je pense que je vais attendre la correction et je la mettrai sur le forum.

Si tu ne veux pas attendre la correction de ton prof :

f(x)=\frac{x^2(6-\frac{3}{x}+\frac{1}{x^2})}{x^2(1-\frac{1}{x^2})}
Et si tu simplifiais par x^2 ?

Je t'avais suggéré de simplifier :

Quelles sont limites, quand de :





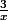
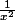
Conclus : vers quoi tend f(x) ?

[Arca13]

Merci Carpate.
Mais en simplifiant comme tu l as dit et en cherchant vers quoi tend x je me retrouve encore face à une forme indéterminée...

[Arca13]

Merci Carpate.
J'ai compris je crois ! F(x) tend vers 6 c'est ça ??

[Carpate]

Merci Carpate.
J'ai compris je crois ! F(x) tend vers 6 c'est ça ??

Oui.
Et tu peux retenir qu'un polynôme se comporte :
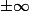
- au voisinage de comme son terme de plus haut degré
- au voisinage de 0 comme son terme de plus bas degré, si est son terme constant

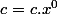
[jonh35230]

Pour la limite en l'infini d'une fraction rationnelle c'est la limite du quotient des termes de plus haut degré

[jonh35230]

Et qu'elle est la limite de f en 2? Conseil:etudie le signe du dénominateur et calculé l'image de 2 par le numérateur

[Arca13]

D'accord ! C'est super ! Je vous remercie infiniment j'ai compris !! :lol3: :lol3:

[jonh35230]

Erreur de lecture remplace la limite de f en 2 par racine carrée de 2 désolé j'ai mal lu l'énoncé et calculé l'image de racine de 2 par le numérateur