(1+j)^100 = j²
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Eskoris
- Membre Naturel
- Messages: 20
- Enregistré le: 20 Oct 2014, 12:19
-
 par Eskoris » 10 Sep 2015, 12:43
par Eskoris » 10 Sep 2015, 12:43
Bonjour,
Comment montrer que (1+j)^100 = j²
J'ai montré que (1+j) = -j²
Qu'est-ce qu'il faudrait faire ensuite ?
Merci
-
Eskoris
- Membre Naturel
- Messages: 20
- Enregistré le: 20 Oct 2014, 12:19
-
 par Eskoris » 10 Sep 2015, 12:54
par Eskoris » 10 Sep 2015, 12:54
si -j² = 1+j, alors (1+j)^100=j² (-j²)^100 = j² et ensuite... ?

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 10 Sep 2015, 13:02
par Sake » 10 Sep 2015, 13:02
Eskoris a écrit:Bonjour,
Comment montrer que (1+j)^100 = j²
J'ai montré que (1+j) = -j²
Qu'est-ce qu'il faudrait faire ensuite ?
Merci
Salut,

, 400 = 4 mod 3 et 100 est pair, donc on conclue facilement.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 10 Sep 2015, 13:20
par chan79 » 10 Sep 2015, 13:20
Salut
On peut aussi utiliser
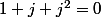
^{100}=j^{200})
et on sait que
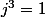
-
Eskoris
- Membre Naturel
- Messages: 20
- Enregistré le: 20 Oct 2014, 12:19
-
 par Eskoris » 10 Sep 2015, 15:23
par Eskoris » 10 Sep 2015, 15:23
Merci,
Je vois claire maintenant :
j^3=1
1+j=-j²
On doit montrer que (1+j)^100 = j²
Donc :
(1+j)^100 = (-j²)^100 = -j^200 = j²*(j^3)^66 = j²*1^66 = j²*1 = j²
Je fais exprès de décomposer autant...
Merci en tout cas

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 10 Sep 2015, 15:59
par chan79 » 10 Sep 2015, 15:59
Eskoris a écrit:Merci,
Je vois claire maintenant :
j^3=1
1+j=-j²
On doit montrer que (1+j)^100 = j²
Donc :
(1+j)^100 = (-j²)^100 = -j^200 = j²*(j^3)^66 = j²*1^66 = j²*1 = j²
Je fais exprès de décomposer autant...
Merci en tout cas
oui, il manque juste une parenthèse
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
