Bonjour,
Je suis bloqué a la question 1 merci de m'aider
Un = 1/1x2+1/2x3+1/3x4+....+1/n(n+1)
1°
Calculer u1,u2,u3,u4
(il y a marqué aussi que Un=Sigma avec n au dessus et k=1 en dessous,facteur de 1/k(k+1)
merci
DM Urgent suites TermS
8 messages
- Page 1 sur 1
Bounder89 a écrit:Bonjour,
Je suis bloqué a la question 1 merci de m'aider
Un = 1/1x2+1/2x3+1/3x4+....+1/n(n+1)
1°
Calculer u1,u2,u3,u4
(il y a marqué aussi que Un=Sigma avec n au dessus et k=1 en dessous,facteur de 1/k(k+1)
merci
trouve a et b tels que
ensuite la somme (avec sigma) va se révéler "télescopique"
WillyCagnes a écrit:bsr
utilise la relation pour la somme des Un
1/n(n+1)=1/n -1/(n+1)
U1=1/2 =1/1 -1/(1+1)
U2=1/2+1/6 = 1/1 -1/(1+1) +[1/(1+1) -1/(1+2) =1/1 -1/3
meme logique pour la suite (telescopage) on obtient
Un=1-1/(n+1)
bsr merci pour vos reponses,je comprends pas ce que vous m'avez dis "telescopique" j'ai pas vu sa en cour donc je supose que je dois pas passer par la =, pourquoi sa serais pas u1= 1/2 u2=1/6 u3=1/12 et u4=1/20 ? en utlisant 1/n(n+1)
Bounder89 a écrit:bsr merci pour vos reponses,je comprends pas ce que vous m'avez dis "telescopique" j'ai pas vu ça en cours donc je suppose que je dois pas passer par la =, pourquoi ça serait pas u1= 1/2 u2=1/6 u3=1/12 et u4=1/20 ? en utilisant 1/n(n+1)
on donne une expression
cette expression permet de simplifier la somme qui passe de n termes à 2 termes.
Salut !
Personnellement, puisqu'on doit calculer pour de petites valeurs de
pour de petites valeurs de  , je ne me prendrais pas la tête : je remplacerais
, je ne me prendrais pas la tête : je remplacerais  successivement par
successivement par 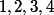 .
.
[CENTER]}.) [/CENTER]
[/CENTER]
Donc :
} = \frac{1}{1(1+1)} = ...) ;
;
} = \frac{1}{1(1+1)}+ \frac{1}{2(2+1)}= ...) ;
;
} = \frac{1}{1(1+1)}+ \frac{1}{2(2+1)}+ \frac{1}{3(3+1)}= ...) ;
;
} = \frac{1}{1(1+1)}+ \frac{1}{2(2+1)}+ \frac{1}{3(3+1)}+ \frac{1}{4(4+1)}= ...) .
.
Remarque : Tu auras peut-être remarque que(n+2)}) , donc tu peux éventuellement t'en servir afin d'éviter de refaire des calculs précédents.
, donc tu peux éventuellement t'en servir afin d'éviter de refaire des calculs précédents.
:+++:
Personnellement, puisqu'on doit calculer
[CENTER]
Donc :
Remarque : Tu auras peut-être remarque que
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Bounder89 a écrit:OK merci beaucoup,maintenant je dois faire sa sur un tableur pour calculer plusieurs termes,sa je sais faire mais dans mon dm je dois programmer un algorithme qui me permettrais d'obtenir les premiers termes sa je sais pas faire..
0 STO S
1 STO N
2 STO N1
INPUT M
WHILE N < M
N*N1 STO I
1/I STO I
S+I STO S
N1 STO N
N1+1 STO N1
ENDWHILE
DISP S
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
