Forme lineaire et opérateur de dérivation

par **bauzau** » 03 Sep 2015, 10:44

Bonjour, préparant l'agrégation interne, je suis tombé sur cet exercice et à vrai dire ... je ne sais même pas comment commencer !

Si qqun a quelques pistes ! Merci

par **Robot** » 03 Sep 2015, 11:01

est une forme linéaire sur

, c'est-à-dire un élément de

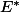
est un endomorphisme de

. Sa transposée

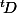
est un endomorphisme de

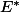
. Peux-tu rappeler la définition de la transposée d'une application linéaire ?

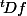
est donc un élément de

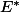
. Appliqué à

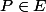
, il produit un réel. Pour savoir lequel, il suffit de suivre scrupuleusement le mode d'emploi, euh ... pardon, les définitions.

par **bauzau** » 03 Sep 2015, 11:29

Merci pour ces indications, je regarde ça cet après midi.

par **mathelot** » 03 Sep 2015, 11:32

.......................

par **Robot** » 03 Sep 2015, 11:43

Euh, mathelot, c'est toi qui avais à faire l'exercice ?

Il est écrit dans la charte :

Note aux correcteurs :
Au cas par cas, lorsqu'il est avéré que l'élève est vraiment perdu dans la résolution d'un problème, qu'il respecte tous les points de la charte (politesse, etc.) et qu'il est de bonne foi (effort de recherche, volonté d'essayer, etc.), il est possible que le correcteur donne une réponse complète. Il est toutefois interdit de le faire si un autre intervenant est en cours d'échange avec l'élève. Dans tous les autres cas, il est demandé au correcteur de guider progressivement l'élève vers la résolution complète de son énoncé.

Lorsqu'un correcteur donne ipso facto la réponse complète à un élève sans que celui-ci n'ait fourni un effort de recherche ou ne paraisse complètement perdu, il est convenu que le modérateur le prévienne par message privé de son comportement contraire à la charte. Au delà de 3 manquements à la charte, le correcteur peut alors se voir sanctionner sous la forme d'une exclusion temporaire de 15 jours ou définitive si le correcteur ne modifie toujours pas son comportement.

par **mathelot** » 03 Sep 2015, 12:02

j'ai effacé. :hum:

par **bauzau** » 03 Sep 2015, 13:51

Ok donc, je vois que j'ai des chapitres à revoir !! A commencer par la transposition d'une application !

D est un endomorphisme de R[X]

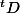
est un endomorphisme de (R[X]*) qui à f associe

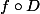
Pour parler "en plus clair" (ou bien en moins avancé)

n'est autre que la fonction f, appliquée à P' ???

et donc

si

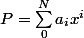
Alors

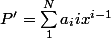
et

C'est ça?

par **mathelot** » 03 Sep 2015, 14:06

bauzau a écrit:Ok donc, je vois que j'ai des chapitres à revoir !! A commencer par la transposition d'une application !

D est un endomorphisme de R[X]
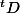
est un endomorphisme de (R[X]*) qui à f associe

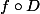
Pour parler "en plus clair" (ou bien en moins avancé) n'est autre que la fonction f, appliquée à P' ???

et donc

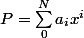
si Alors

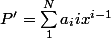
et

C'est ça?

oui, on peut l'écrire avec des Diracs

par **Robot** » 03 Sep 2015, 14:10

bauzau a écrit:Pour parler "en plus clair" (ou bien en moins avancé) n'est autre que la fonction f, appliquée à P' ???

Ce n'est pas plus clair, c'est juste moins correct.

Si

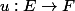
est une application linéaire, sa transposée

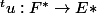
est l'application linéaire définie par

.
Autrement dit,

est la forme linéaire sur

définie par

pour tout

.

par **bauzau** » 03 Sep 2015, 14:30

Merci pour vos réponses, ça m'éclaire !

par **Sake** » 04 Sep 2015, 10:05

Robot a écrit:Ce n'est pas plus clair, c'est juste moins correct.

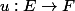
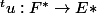
Si est une application linéaire, sa transposée est l'application linéaire définie par
.
Autrement dit, est la forme linéaire sur définie par pour tout .

[TROLL]

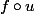
peut prêter à confusion !! :ptdr: (oui, je suis parti)
[\TROLL]

Forme lineaire et opérateur de dérivation

forme lineaire et opérateur de dérivation

Qui est en ligne