Intégrale quotient exponentielle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Lapin31
- Membre Naturel
- Messages: 10
- Enregistré le: 29 Aoû 2015, 16:12
-
 par Lapin31 » 29 Aoû 2015, 16:17
par Lapin31 » 29 Aoû 2015, 16:17
Bonjour, j'ai un travail à rendre pour la rentrée dans lequel j'ai une intégrale qui me pose problème , l'intégrale est la suivante : intégrale de [ ( e^3x + e^x ) / ( e^2x + e^x + 2 ) ]
Je pense que cette intégrale est de la forme u'(x) / u(x) , mais je n'arrive pas à trouver un facteur pour que ( e^3x + e^x) soit égale a 2e^2x + e^x.
Merci de votre aide !
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 29 Aoû 2015, 16:55
par Carpate » 29 Aoû 2015, 16:55
Lapin31 a écrit:Bonjour, j'ai un travail à rendre pour la rentrée dans lequel j'ai une intégrale qui me pose problème , l'intégrale est la suivante : intégrale de [ ( e^3x + e^x ) / ( e^2x + e^x + 2 ) ]
Je pense que cette intégrale est de la forme u'(x) / u(x) , mais je n'arrive pas à trouver un facteur pour que ( e^3x + e^x) soit égale a 2e^2x + e^x.
Merci de votre aide !
Changement de variable
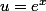
puis décomposition en éléments simples

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 29 Aoû 2015, 17:05
par zygomatique » 29 Aoû 2015, 17:05
salut
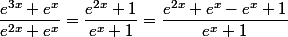
....
:ptdr:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Lapin31
- Membre Naturel
- Messages: 10
- Enregistré le: 29 Aoû 2015, 16:12
-
 par Lapin31 » 29 Aoû 2015, 18:29
par Lapin31 » 29 Aoû 2015, 18:29
Carpate a écrit:Changement de variable
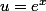
puis décomposition en éléments simples
J'ai pensé à l'idée de changer de variables mais je n'y arrive absolument pas non plus
-
Lapin31
- Membre Naturel
- Messages: 10
- Enregistré le: 29 Aoû 2015, 16:12
-
 par Lapin31 » 29 Aoû 2015, 18:32
par Lapin31 » 29 Aoû 2015, 18:32
zygomatique a écrit:salut
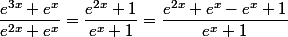
....
:ptdr:
Vous avez simplifié par e^x puis ajoute e^x pour le soustraire mais je ne vois pas l'utilité au niveau de cette intégrale :/

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 29 Aoû 2015, 18:54
par zygomatique » 29 Aoû 2015, 18:54
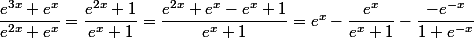
ou
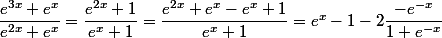
dans les deux cas le calcul d'une primitive est trivial ....
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 29 Aoû 2015, 20:08
par Pisigma » 29 Aoû 2015, 20:08
Lapin31 a écrit:Bonjour, j'ai un travail à rendre pour la rentrée dans lequel j'ai une intégrale qui me pose problème , l'intégrale est la suivante : intégrale de [ ( e^3x + e^x ) / ( e^2x + e^x + 2 ) ]
Je pense que cette intégrale est de la forme u'(x) / u(x) , mais je n'arrive pas à trouver un facteur pour que ( e^3x + e^x) soit égale a 2e^2x + e^x.
Merci de votre aide !
Bonsoir,
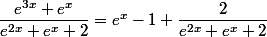

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 29 Aoû 2015, 23:34
par zygomatique » 29 Aoû 2015, 23:34
Pisigma a écrit:Bonsoir,
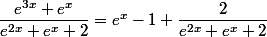
certes ... mais ça n'est pas suffisant (il faut encore faire un effort) ....
ce qui n'est pas le cas des deux expressions que je donne ...
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 29 Aoû 2015, 23:36
par zygomatique » 29 Aoû 2015, 23:36
damned .... :mur: je viens de me rendre compte que j'e n'ai pas pris le bon dénominateur ....

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 30 Aoû 2015, 07:11
par Pisigma » 30 Aoû 2015, 07:11
zygomatique a écrit:certes ... mais ça n'est pas suffisant (il faut encore faire un effort) ....
ce qui n'est pas le cas des deux expressions que je donne ...
:lol3:
Bonjour,
pour la fraction, il reste à poser e^x=t. Ensuite décomposition en fractions simples...
-
Cauchy2010
- Membre Relatif
- Messages: 141
- Enregistré le: 18 Juil 2015, 21:23
-
 par Cauchy2010 » 30 Aoû 2015, 09:19
par Cauchy2010 » 30 Aoû 2015, 09:19
J'ai une meilleure suggestion : IPP, à creuser, ça semble plus prometteur.
-
Lapin31
- Membre Naturel
- Messages: 10
- Enregistré le: 29 Aoû 2015, 16:12
-
 par Lapin31 » 30 Aoû 2015, 09:48
par Lapin31 » 30 Aoû 2015, 09:48
Pisigma a écrit:Bonjour,
pour la fraction, il reste à poser e^x=t. Ensuite décomposition en fractions simples...
Ce qui nous donne 1/ x^2+x+2 , mais quelle est la primitive de cette fraction ? J'ai vu sur internet l'utilisation de l'arctan(x) mais je ne maîtrise absolument pas cette fonction
-
Lapin31
- Membre Naturel
- Messages: 10
- Enregistré le: 29 Aoû 2015, 16:12
-
 par Lapin31 » 30 Aoû 2015, 09:49
par Lapin31 » 30 Aoû 2015, 09:49
zygomatique a écrit:damned .... :mur: je viens de me rendre compte que j'e n'ai pas pris le bon dénominateur ....

Oui le dénominateur est e^2x +e^x +2 , sinon j'avais trouvé votre démarche mais elle ne fonctionne pas ducoup pour ma fonction

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 30 Aoû 2015, 09:50
par zygomatique » 30 Aoû 2015, 09:50
oui c'est cela ...
écris le trinome sous forme canonique et fais le bon changement de variable ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Lapin31
- Membre Naturel
- Messages: 10
- Enregistré le: 29 Aoû 2015, 16:12
-
 par Lapin31 » 30 Aoû 2015, 09:50
par Lapin31 » 30 Aoû 2015, 09:50
Cauchy2010 a écrit:J'ai une meilleure suggestion : IPP, à creuser, ça semble plus prometteur.
Ipp ? C'est à dire ?
-
Lapin31
- Membre Naturel
- Messages: 10
- Enregistré le: 29 Aoû 2015, 16:12
-
 par Lapin31 » 30 Aoû 2015, 10:08
par Lapin31 » 30 Aoû 2015, 10:08
zygomatique a écrit:oui c'est cela ...
écris le trinome sous forme canonique et fais le bon changement de variable ...
Si on pose e^x = X , on obtient 1/ X^2 + X + 2 ce qui équivaut à 1 / ( X + 1/2 )^2 + 7/4 , et comment je fais pour trouver la primitive de 1/ la forme canonique ? Es ce arctan ( x+1/2 ) ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 30 Aoû 2015, 12:33
par zygomatique » 30 Aoû 2015, 12:33
pour utiliser arctan il faut écrire ce quotient sous la forme u'/(1 + u²) ...
or tu as 7/4 ... donc ... ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 30 Aoû 2015, 13:08
par Carpate » 30 Aoû 2015, 13:08
Lapin31 a écrit:Si on pose e^x = X , on obtient 1/ X^2 + X + 2 ce qui équivaut à 1 / ( X + 1/2 )^2 + 7/4 , et comment je fais pour trouver la primitive de 1/ la forme canonique ? Es ce arctan ( x+1/2 ) ?
Non
^2+7}{4}=\frac74[1+\frac47(2X+1)^2]=\frac74[1+(\frac{2(2X+1)}{\sqrt7})^2])
}{\sqrt7})
EDIT :
J'ai zapé le changement
}{\sqrt7})
Il faut tenir compte de
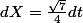
-
Cauchy2010
- Membre Relatif
- Messages: 141
- Enregistré le: 18 Juil 2015, 21:23
-
 par Cauchy2010 » 30 Aoû 2015, 16:28
par Cauchy2010 » 30 Aoû 2015, 16:28
Lapin31 a écrit:Ipp ? C'est à dire ?
Intégration par parties ...
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 31 Aoû 2015, 07:36
par Pisigma » 31 Aoû 2015, 07:36
Lapin31 a écrit:Si on pose e^x = X , on obtient 1/ X^2 + X + 2 ce qui équivaut à 1 / ( X + 1/2 )^2 + 7/4 , et comment je fais pour trouver la primitive de 1/ la forme canonique ? Es ce arctan ( x+1/2 ) ?
Bonjour,
})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
