Bonjour,
s'il vous plait pouvez vous m'aider à résoudre ces équations. Je suis dessus depuis un mois je n'arrive pas :mur: :mur:
1) y' + y² =x
2) y'= x/(x+y)
Équation différentielle coriace
11 messages
- Page 1 sur 1
Salut !
Pour la première déjà :
1) Trouve une solution particulière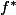 de cette équation différentielle.
de cette équation différentielle.
2) Résous l'équation homogène associée .
.
Pour cela, effectue le changement de variable et montre que résoudre
et montre que résoudre  revient à résoudre
revient à résoudre  . Déduis-en la forme générale de
. Déduis-en la forme générale de  , puis de
, puis de  . On notera
. On notera  la forme générale des solutions, où
la forme générale des solutions, où  désigne la constante.
désigne la constante.
Conclusion : l'ensemble des solutions sera formé de toutes les fonctions de la forme .
.
:+++:
Pour la première déjà :
1) Trouve une solution particulière
2) Résous l'équation homogène associée
Pour cela, effectue le changement de variable
Conclusion : l'ensemble des solutions sera formé de toutes les fonctions de la forme
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Salut !
Pour la première :
1) Trouve une solution particulière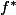 de cette équation différentielle.
de cette équation différentielle.
2) Résous l'équation homogène associée .
.
Pour cela, effectue le changement de variable et montre que résoudre
et montre que résoudre  revient à résoudre
revient à résoudre  . Déduis-en la forme générale de
. Déduis-en la forme générale de  , puis de
, puis de  . On notera
. On notera  la forme générale des solutions, où
la forme générale des solutions, où  désigne une constante réelle.
désigne une constante réelle.
Conclusion : l'ensemble des solutions sera formé de toutes les fonctions de la forme .
.
:+++:
Pour la première :
1) Trouve une solution particulière
2) Résous l'équation homogène associée
Pour cela, effectue le changement de variable
Conclusion : l'ensemble des solutions sera formé de toutes les fonctions de la forme
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Salut !
Pour la première :
1) Trouve une solution particulièrede cette équation différentielle.
2) Résous l'équation homogène associée.
Pour cela, effectue le changement de variableet montre que résoudre
revient à résoudre
. Déduis-en la forme générale de
, puis de
. On notera
la forme générale des solutions, où
désigne une constante réelle.
Conclusion : l'ensemble des solutions sera formé de toutes les fonctions de la forme.
:+++:
Capitaine nuggets, penses-tu vraiment que si
2)
y'= x/(x+y)
Poser y = u.x
y' = u + u'.x
u + u'.x = x/(x + ux)
u + u'.x = 1/(1 + u)
u'.x = 1/(1 + u) - u
u'.x = (1 - u - u²)/(1+u)
du * (1+u)/(1 - u - u²) = dx/x
On intègre (décomposition de fraction rationnelle pour le membre de gauche) :
(1/10).(V5 - 5).ln|2u + V5 + 1| - (1/10).(5 + V5).ln|-2u + V5 - 1| = ln|k.x|
(1/10).(V5 - 5).ln|2y/x + V5 + 1| - (1/10).(5 + V5).ln|-2y/x + V5 - 1| = ln|k.x|
C'est une équation fonctionnelle liant x et y
(il y a probablement des conditions de validité à introduire de-ci de-là dans ce que j'ai écrit)
:zen:
y'= x/(x+y)
Poser y = u.x
y' = u + u'.x
u + u'.x = x/(x + ux)
u + u'.x = 1/(1 + u)
u'.x = 1/(1 + u) - u
u'.x = (1 - u - u²)/(1+u)
du * (1+u)/(1 - u - u²) = dx/x
On intègre (décomposition de fraction rationnelle pour le membre de gauche) :
(1/10).(V5 - 5).ln|2u + V5 + 1| - (1/10).(5 + V5).ln|-2u + V5 - 1| = ln|k.x|
(1/10).(V5 - 5).ln|2y/x + V5 + 1| - (1/10).(5 + V5).ln|-2y/x + V5 - 1| = ln|k.x|
C'est une équation fonctionnelle liant x et y
(il y a probablement des conditions de validité à introduire de-ci de-là dans ce que j'ai écrit)
:zen:
Un logiciel de calcul formel donne comme solution à la première équation une fonction de la forme  , où
, où  est solution de l'équation différentielle
est solution de l'équation différentielle  , c.-à-d.
, c.-à-d.  est combinaison linéaire des fonctions d'Airy Ai et Bi.
est combinaison linéaire des fonctions d'Airy Ai et Bi.
En effet si est solution de
est solution de  , en prenant pour
, en prenant pour  l'exponentielle d'une primitive de
l'exponentielle d'une primitive de  on a
on a  et
et 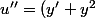u=xu) . Réciproquement, si
. Réciproquement, si  est une solution de
est une solution de  , alors en posant
, alors en posant  on obtient
on obtient  et donc
et donc  .
.
Dans tout ceci on n'a pas fait attention aux intervalles sur lesquels ces solutions sont définies.
En effet si
Dans tout ceci on n'a pas fait attention aux intervalles sur lesquels ces solutions sont définies.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
