Bonjour à tous
J'ai un doute concernant mon raisonnement
Soit la suite définie par : Un=a^n ; a un réel (appartint à R)
1) Un est elle géométrique
2) est elle décroissante
3) pour a dans (-1;1) Un converge t-elle vers 0.
Réponses
1) Un est géométrique de raison a car : U(n+1)=Un*a :id:
2) U(n+1)-Un = a^n(a-1) je dis qu'il faut discuter 3 cas :
_ a supérieur ou égal à 1, U(n+1) sup Un donc Un croisante
_ 0 < a <=1 U(n+1) < Un donc Un décroissante
_ a < 0 deux cas se présente : n paire U(n+1) < Un décroissante
n impaire U(n+1) sup Un croissante
3) je peux rien dire car selon la question 2) la monotonie de U dépend de a et de la parité de n. :triste:
Qu'est ce que vous en pensez merci d'avance.
étude de suite
4 messages
- Page 1 sur 1
Bonjour,
1) Ok
2) On te demande si la suite un est décroissante et non d'étudier tous les cas possible.
Dans le cas présent tu peux simplement dire que la suite un est décroissante si et seulement si 0 1 :
 donc un est croissante
donc un est croissante
* Pour a = 1 :
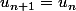 donc un est constante
donc un est constante
* Pour 0 u_n[/tex] MAIS
Donc tu ne peux pas conclure sur la monotonie de la suite.
3) Est-ce que a appartient à [-1; 1] ou à ]-1; 1[ ?
* Si -1 < a < 1 que peux-tu dire de :
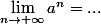
* Si -1 <= a <= 1 que peux-tu dire quand :
^n = ...)
^n = ...)
Tu devrais pouvoir répondre à la question
1) Ok
2) On te demande si la suite un est décroissante et non d'étudier tous les cas possible.
Dans le cas présent tu peux simplement dire que la suite un est décroissante si et seulement si 0 1 :
* Pour a = 1 :
* Pour 0 u_n[/tex] MAIS
Donc tu ne peux pas conclure sur la monotonie de la suite.
3) Est-ce que a appartient à [-1; 1] ou à ]-1; 1[ ?
* Si -1 < a < 1 que peux-tu dire de :
* Si -1 <= a <= 1 que peux-tu dire quand :
Tu devrais pouvoir répondre à la question
Bonjour à tous
J'ai un doute concernant mon raisonnement
Soit la suite définie par : Un=a^n ; a un réel (appartint à R)
1) Un est elle géométrique
2) est elle décroissante
3) pour a dans (-1;1) Un converge t-elle vers 0.
Réponses
1) Un est géométrique de raison a car : U(n+1)=Un*a :id:
Un+1/Un=a donc (Un) est geometrique
2) U(n+1)-Un = a^n(a-1) je dis qu'il faut discuter 3 cas :
_ a supérieur ou égal à 1, U(n+1) sup Un donc Un croisante
_ 0 +infini) Un=U0 Un converge vers ...
Si a dans ]1;+infini[ si Un>0 la suite est croissante >0
Si Un 0 et 0 la suite est decroissante >0
Si Un1 la suite diverge
Si a=1 la suite tend vers ....
Qu'est ce que vous en pensez merci d'avance
J'ai un doute concernant mon raisonnement
Soit la suite définie par : Un=a^n ; a un réel (appartint à R)
1) Un est elle géométrique
2) est elle décroissante
3) pour a dans (-1;1) Un converge t-elle vers 0.
Réponses
1) Un est géométrique de raison a car : U(n+1)=Un*a :id:
Un+1/Un=a donc (Un) est geometrique
2) U(n+1)-Un = a^n(a-1) je dis qu'il faut discuter 3 cas :
_ a supérieur ou égal à 1, U(n+1) sup Un donc Un croisante
_ 0 +infini) Un=U0 Un converge vers ...
Si a dans ]1;+infini[ si Un>0 la suite est croissante >0
Si Un 0 et 0 la suite est decroissante >0
Si Un1 la suite diverge
Si a=1 la suite tend vers ....
Qu'est ce que vous en pensez merci d'avance
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
