TS -> calcul de limites
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
misterg94
- Membre Naturel
- Messages: 43
- Enregistré le: 23 Sep 2006, 16:34
-
 par misterg94 » 24 Sep 2006, 13:52
par misterg94 » 24 Sep 2006, 13:52
Salut à tous !
Déterminer les limites suivantes :
A=Lim xsin(1/x) quand x->0
On pose X=1/x x=1/X
*LimX quand x->0+ =0+
*Lim(1/X)sinX quand X->0+ =(sinX)/X = +oo
donc Lim xsin(1/x) quand x->0 = +oo
B=Lim V((2x+1)/(x-1)) quand x->+oo
Je pense avoir trouvé :
On pose X=(2x+1)/(x-1)
*LimX quand x->+oo = ((2x+1)/(x-1))((x+1)/(x+1))
= (2x²+3x+1)/(x²-1)
=(2x²)/(x²)
= 2
*Lim V(X) quand X->2 = V(2)
donc Lim V((2x+1)/(x-1)) quand x->+oo = V(2)
C=Lim V(x²-4x+9)+x-3 quand x->-oo
On pose X=x²-4x+9
*LimX quand x->-oo = Lim x² = -oo
*LimV(X) quand X->-oo = j'ai du faire une erreur avant car cala ne peut pas tendre vers -oo sous une racine ? non ?
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 24 Sep 2006, 13:58
par Sdec25 » 24 Sep 2006, 13:58
Salut
Pour la première il faut encadrer sin(x)
Pour la B il faut factoriser par x en haut et en bas.
Pour la C essaie de multiplier par la quantité conjuguée.
-
misterg94
- Membre Naturel
- Messages: 43
- Enregistré le: 23 Sep 2006, 16:34
-
 par misterg94 » 24 Sep 2006, 14:03
par misterg94 » 24 Sep 2006, 14:03
Sdec25 a écrit:Pour la première il faut encadrer sin(x)
-1<SinX<1
-1/X<(sinX)/x<1/X
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 24 Sep 2006, 14:06
par Sdec25 » 24 Sep 2006, 14:06
Tu n'es pas obligé de faire un changement de variable :
-1 < sin(1/x) < 1
-x < x sin(1/x) < x, donc la limite quand x tend vers 0 ?
-
misterg94
- Membre Naturel
- Messages: 43
- Enregistré le: 23 Sep 2006, 16:34
-
 par misterg94 » 24 Sep 2006, 14:07
par misterg94 » 24 Sep 2006, 14:07
Sdec25 a écrit:Tu n'es pas obligé de faire un changement de variable :
-1 < sin(1/x) < 1
-x < x sin(1/x) < x, donc la limite quand x tend vers 0 ?
ok et après j'applique le théorème des gendarmes !
-
misterg94
- Membre Naturel
- Messages: 43
- Enregistré le: 23 Sep 2006, 16:34
-
 par misterg94 » 24 Sep 2006, 14:11
par misterg94 » 24 Sep 2006, 14:11
[donc lim xsin(1/x) = 0 car lim -x = 0 et lim x = 0] quand x->0
-
misterg94
- Membre Naturel
- Messages: 43
- Enregistré le: 23 Sep 2006, 16:34
-
 par misterg94 » 24 Sep 2006, 14:16
par misterg94 » 24 Sep 2006, 14:16
Sdec25 a écrit:Pour la B il faut factoriser par x en haut et en bas.
Mais c'est bon aussi avec la méthode que j'ai fait non ?
Car lorsque je factorise par x en haut et en bas, la limite et 2/1, donc 2 !
Non ?
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 24 Sep 2006, 14:26
par Sdec25 » 24 Sep 2006, 14:26
La première est juste.
Pour la B tu as fait un peu compliqué, tu aurais pu dire directement que
}{x(1-1/x)}})
donc la limite est racine(2)
-
misterg94
- Membre Naturel
- Messages: 43
- Enregistré le: 23 Sep 2006, 16:34
-
 par misterg94 » 24 Sep 2006, 14:32
par misterg94 » 24 Sep 2006, 14:32
Sdec25 a écrit:La première est juste.
Pour la B tu as fait un peu compliqué, tu aurais pu dire directement que
}{x(1-1/x)}})
donc la limite est racine(2)
d'accord !
-
misterg94
- Membre Naturel
- Messages: 43
- Enregistré le: 23 Sep 2006, 16:34
-
 par misterg94 » 24 Sep 2006, 15:00
par misterg94 » 24 Sep 2006, 15:00
Sdec25 a écrit:Pour la C essaie de multiplier par la quantité conjuguée.
en fait ce qui me pose problème c'est la limite de x²-4x+9 quand x->-oo ca me domme une limite indéterminé...
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 24 Sep 2006, 15:05
par Sdec25 » 24 Sep 2006, 15:05
Justement il faut multiplier par la quantité conjuguée :
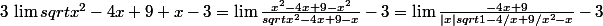
-
misterg94
- Membre Naturel
- Messages: 43
- Enregistré le: 23 Sep 2006, 16:34
-
 par misterg94 » 24 Sep 2006, 15:08
par misterg94 » 24 Sep 2006, 15:08
Sdec25 a écrit:Justement il faut multiplier par la quantité conjuguée :
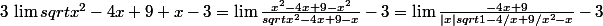
oula je suis perdu !
-
misterg94
- Membre Naturel
- Messages: 43
- Enregistré le: 23 Sep 2006, 16:34
-
 par misterg94 » 24 Sep 2006, 15:10
par misterg94 » 24 Sep 2006, 15:10
Sdec25 a écrit:Justement il faut multiplier par la quantité conjuguée :
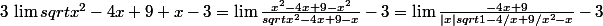
pourquoi il y a une valeur absolu en bas ?
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 24 Sep 2006, 15:12
par Sdec25 » 24 Sep 2006, 15:12
Parce que racine(x²) = |x|
Dans ce cas ça nous arrange car |x|-x équivaut à -2x au voinage de -inf
-
misterg94
- Membre Naturel
- Messages: 43
- Enregistré le: 23 Sep 2006, 16:34
-
 par misterg94 » 24 Sep 2006, 15:23
par misterg94 » 24 Sep 2006, 15:23
Sdec25 a écrit:Parce que racine(x²) = |x|
Dans ce cas ça nous arrange car |x|-x équivaut à -2x au voinage de -inf
et qu'est ce qu'on fait de ce qu'il y a sous la racine on en tient pas compte ?
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 24 Sep 2006, 15:25
par Sdec25 » 24 Sep 2006, 15:25
Si, on calcule la limite en faisant une division.
-
misterg94
- Membre Naturel
- Messages: 43
- Enregistré le: 23 Sep 2006, 16:34
-
 par misterg94 » 24 Sep 2006, 15:42
par misterg94 » 24 Sep 2006, 15:42
Sdec25 a écrit:Si, on calcule la limite en faisant une division.
oki merci beaucoup de ton aide !
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 24 Sep 2006, 15:55
par Sdec25 » 24 Sep 2006, 15:55
de rien :we:
Tu trouves combien finalement ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
