Bonjour
f(x)=(x-1)*e^(1/x) sur]-oo;0[
Résultats des premières questions:
f est strictement croissante sur ]-oo;0[
lim f(x)=-oo en -oo et lim f(x)=0 en 0
f(x)>x sur ]-oo;0[
On définit la suite U par U0=-3 et pourt tout n, U(n+1)=f(Un)
On démontre que:
Un0 (là j'utilise le fait que Un et U(n+1) sont de même signe car U(n+1)-Un ne donne rien...)
U(n+1)/Un=((Un-1)*e^(1/Un))/Un=1-1/Un*e^(1/Un)
1-1/Un*e^(1/Un)>1 car Un<0
donc U croissante
b) montrer que U converge et calculer sa limite
U croissante et Un<0 alors U converge
Soit l sa limite
l=(l-1)*e^(1/l)
Là je bloque pour résoudre cette équation.
Merci pour vos commentaires
Suites
12 messages
- Page 1 sur 1
Salut !
Je rejoins CBMaths_prof, l'équation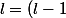e^{\frac 1 l}) ne peut pas être résolue algébriquement du fait qu'on ne peut pas isoler
ne peut pas être résolue algébriquement du fait qu'on ne peut pas isoler  .
.
Pour résoudre l'équation, tu dois déterminant quand est-ce que la fonction=f(x)-x) s'annule en étudiant ses variations.
s'annule en étudiant ses variations.
Je rejoins CBMaths_prof, l'équation
Pour résoudre l'équation, tu dois déterminant quand est-ce que la fonction
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Il doit y avoir une erreur dans l'ennoncé ,on fait ce qu on doit montrer c est que f(x) x
U(n) est croissante et majorée par 0 donc elle converge et sa limite est 0
En la traçant on trouve bien ce résultat
voila les points
(-0.5; -0,2)
(-1 ; -0,73)
(-2 ; -1,82)
(-3 ; -2,86)
Voila vérifiez avec moi svp
U(n) est croissante et majorée par 0 donc elle converge et sa limite est 0
En la traçant on trouve bien ce résultat
voila les points
(-0.5; -0,2)
(-1 ; -0,73)
(-2 ; -1,82)
(-3 ; -2,86)
Voila vérifiez avec moi svp
Bonjour
On démontre bien que f(x)>x sur ]-oo;0[
D'ailleurs le graphique de f et de y=x nous montre bien que la courbe de f est au dessus de la droite (d) y=x
J'ai une idée, ça vaut ce que ça vaut:
Puisque:
f est strictement croissante sur ]-oo;0[
lim f(x)=-oo en -oo et lim f(x)=0 en 0
lim x en 0 est 0
f(x)>x sur ]-oo;0[
Cela nous prouve bien que Cf et (d) converge vers 0 (peut être le mot converge est impropre ici) et on peut en déduire que lim U=0
On démontre bien que f(x)>x sur ]-oo;0[
D'ailleurs le graphique de f et de y=x nous montre bien que la courbe de f est au dessus de la droite (d) y=x
J'ai une idée, ça vaut ce que ça vaut:
Puisque:
f est strictement croissante sur ]-oo;0[
lim f(x)=-oo en -oo et lim f(x)=0 en 0
lim x en 0 est 0
f(x)>x sur ]-oo;0[
Cela nous prouve bien que Cf et (d) converge vers 0 (peut être le mot converge est impropre ici) et on peut en déduire que lim U=0
Bonjour Chan
Oui c'est plus simple à l'aide de de pour montrer la croissance de U
Ce que j'ai fait, ci dessous, est ce correcte ?
Oui c'est plus simple à l'aide de de pour montrer la croissance de U
Ce que j'ai fait, ci dessous, est ce correcte ?
a) Etudier les variations de U
Puisque U(n+1)0 (là j'utilise le fait que Un et U(n+1) sont de même signe car U(n+1)-Un ne donne rien...)
U(n+1)/Un=((Un-1)*e^(1/Un))/Un=1-1/Un*e^(1/Un)
1-1/Un*e^(1/Un)>1 car Un<0
donc U croissante
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

