Les nombres initiateurs
59 messages
- Page 3 sur 3 - 1, 2, 3
Bonsoir,
Pour ta première question:
On raisonne par l'absurde, on suppose qu'un entier I (où I>0) est initiateur de n! et (n+1)!. Il existe donc deux entiers h et h' tels que h<h' et tel que:
I+(I+1)+...+(I+h)=n!
I+(I+1)+...+(I+h')=(n+1)!
Soit encore:
I+(I+1)+...+(I+h')=(n+1)(I+(I+1)+...+(I+h))
D'où, en développant et en ramenant dans le même membre:
(n+1-1)I+(n+1-1)(I+1)+...+(n+1-1)(I+h)+(I+h+1)+...+(I+h')=0
Il s'agit d'une somme nulle d'entiers naturels, donc tous les entiers sommés sont nuls, on en déduit alors que:
nI=0
Puisque I est strictement positif, on a:
n=0
On remarque que 0!=1!=1 et que ces deux factorielles n'ont pas d'initiateurs, ce qui est absurde.
Voilà voilà, en espérant ne pas avoir fait de bêtises..!
Bonne soirée !
Pour ta première question:
On raisonne par l'absurde, on suppose qu'un entier I (où I>0) est initiateur de n! et (n+1)!. Il existe donc deux entiers h et h' tels que h<h' et tel que:
I+(I+1)+...+(I+h)=n!
I+(I+1)+...+(I+h')=(n+1)!
Soit encore:
I+(I+1)+...+(I+h')=(n+1)(I+(I+1)+...+(I+h))
D'où, en développant et en ramenant dans le même membre:
(n+1-1)I+(n+1-1)(I+1)+...+(n+1-1)(I+h)+(I+h+1)+...+(I+h')=0
Il s'agit d'une somme nulle d'entiers naturels, donc tous les entiers sommés sont nuls, on en déduit alors que:
nI=0
Puisque I est strictement positif, on a:
n=0
On remarque que 0!=1!=1 et que ces deux factorielles n'ont pas d'initiateurs, ce qui est absurde.
Voilà voilà, en espérant ne pas avoir fait de bêtises..!
Bonne soirée !
L'espression générale des ni n initiateurs de n! peut s'écrire:
ni=n!/(2k+1)-k ou n!/(2^(p+1)*(2k+1))-(2^(p+1)*(2k+1)-1)/2. Avec 2^p qui est la parité de n!. Les termes 2k+1 ou 2^(p+1)*(2k+1) doivent être =0.
On peut les calculer directement à partir des diviseurs de n!, ou encore, pour un bon nombre d'entre eux, les retrouver à partir des (n-1)i.
NB:
Je ne crois pas que 1 soit initiateur une infinité de fois.
Dans l'expression 2n!=k(k+1), k et k+1 sont premiers entre eux. Ceci signifie qu'on doit classer toutes les puissances d'un nombre premier soit dans k, soit dans k+1. Cela réduit beaucoup les possibilités de trouver une décomposition en k (k+1). Il semblerait qu'il n'y ait pas d'autres factorielles que 3! et 5!
ni=n!/(2k+1)-k ou n!/(2^(p+1)*(2k+1))-(2^(p+1)*(2k+1)-1)/2. Avec 2^p qui est la parité de n!. Les termes 2k+1 ou 2^(p+1)*(2k+1) doivent être =0.
On peut les calculer directement à partir des diviseurs de n!, ou encore, pour un bon nombre d'entre eux, les retrouver à partir des (n-1)i.
NB:
Je ne crois pas que 1 soit initiateur une infinité de fois.
Dans l'expression 2n!=k(k+1), k et k+1 sont premiers entre eux. Ceci signifie qu'on doit classer toutes les puissances d'un nombre premier soit dans k, soit dans k+1. Cela réduit beaucoup les possibilités de trouver une décomposition en k (k+1). Il semblerait qu'il n'y ait pas d'autres factorielles que 3! et 5!
Bonjour !
J'ai une propriété qui pourrait servir: Tout entier naturel supérieur ou égal à 2 est initiateur d'au plus une factorielle.
La démonstration est analogue à celle que j'ai faite avant:
On considère deux entiers et
et 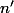 tels que
tels que 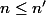 . On suppose que
. On suppose que  et
et 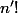 ont un initiateur commun, c'est-à-dire un entier I ainsi que deux entiers
ont un initiateur commun, c'est-à-dire un entier I ainsi que deux entiers  et
et 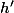 tels que:
tels que:
[CENTER]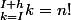 [/CENTER]
[/CENTER]
et:
[CENTER]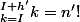 [/CENTER]
[/CENTER]
D'où:
[CENTER]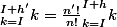 [/CENTER]
[/CENTER]
Soit:
[CENTER]k+\bigsum_{k=I+h}^{I+h'} k=0) [/CENTER]
[/CENTER]
Il s'agit d'une somme d'entiers naturels nulle, donc tous les entiers sommés sont nuls. D'où:
[CENTER]I=0) [/CENTER]
[/CENTER]
Or I est supposé non nul, on en déduit que:
[CENTER]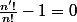 [/CENTER]
[/CENTER]
Donc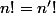 .
.
Puisque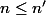 , on en déduit que soit
, on en déduit que soit 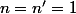 , soit
, soit 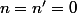 , soit
, soit  et
et 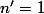 .
.
Ainsi,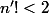 , donc
, donc 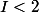 .
.
Par contraposé, si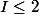 , alors il est initiateur d'au plus une factorielle.
, alors il est initiateur d'au plus une factorielle.
(Ce qui signifie que si on prend deux factorielles supérieures à 2, alors leurs initiateurs sont tous distincts)
Bonne journée ! :we:
J'ai une propriété qui pourrait servir: Tout entier naturel supérieur ou égal à 2 est initiateur d'au plus une factorielle.
La démonstration est analogue à celle que j'ai faite avant:
On considère deux entiers
[CENTER]
et:
[CENTER]
D'où:
[CENTER]
Soit:
[CENTER]
Il s'agit d'une somme d'entiers naturels nulle, donc tous les entiers sommés sont nuls. D'où:
[CENTER]
Or I est supposé non nul, on en déduit que:
[CENTER]
Donc
Puisque
Ainsi,
Par contraposé, si
(Ce qui signifie que si on prend deux factorielles supérieures à 2, alors leurs initiateurs sont tous distincts)
Bonne journée ! :we:
Waax22951 :: dans la formule qui suit ton "soit" .... ne serait-ce pas un moins ?
S(i, p) = i + i + 1 + ... + i + p
soit n (p + 1)(2i + p) = 2n!
S(i, p + q) = m! (p + q + 1)(2i + p + q) = 2m!
m!(p + 1)(2i + p) = n!(p + q + 1)(2i + p + q) [m!/n! - 1](p + 1)(2i + p) = q(2i + 2p + 1)
ou encore (m! - n!)(p + 1)(2i + p) = n!q(2i + 2p + 1)
je ne vois pas pourquoi cette équation n'aurait pas de solution ....
de même :: n! = S(i, p) = S(j, q) (p + 1)(2i + p) = (q + 1)(2j + q)
je ne vois pas pourquoi cette équation n'aurait pas de solution ....
S(i, p) = i + i + 1 + ... + i + p
soit n (p + 1)(2i + p) = 2n!
S(i, p + q) = m! (p + q + 1)(2i + p + q) = 2m!
m!(p + 1)(2i + p) = n!(p + q + 1)(2i + p + q) [m!/n! - 1](p + 1)(2i + p) = q(2i + 2p + 1)
ou encore (m! - n!)(p + 1)(2i + p) = n!q(2i + 2p + 1)
je ne vois pas pourquoi cette équation n'aurait pas de solution ....
de même :: n! = S(i, p) = S(j, q) (p + 1)(2i + p) = (q + 1)(2j + q)
je ne vois pas pourquoi cette équation n'aurait pas de solution ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Mario2015 a écrit:Si on se resumait on dirait que les nombres initiateurs sont les nombres solutions a une equation diophantienne de cette forme :
2*(n!)=(I+F)(F-I+1) ou I est le nombre initiateur et F le dernier terme d`une suite arithmetique de raison 1.
J`ai oublie la contrainte F>I
Avec un I fixe l`equation peut admettre plusieurs F possibles et donc plusieurs n!
Donc un initiateur peut conduire a plusieurs factorielles.
La relation 2*p!=(I+F)(F-I+1) est équivalente à une autre, mais montre peut être encore plus la difficulté du problème car elle montre que la décomposition en facteurs premiers de (I-F+1)}{2}) doit être celle de factorielle p; je ne dis pas que c'est impossible puisque:
doit être celle de factorielle p; je ne dis pas que c'est impossible puisque:
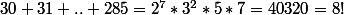 , mais les puissances de 2 augmentent très vite, ce qui rend une telle coïncidence relativement improbable.
, mais les puissances de 2 augmentent très vite, ce qui rend une telle coïncidence relativement improbable.
Bonjour !
En effet, je me suis planté en transformant un "+" en "-", mais du coup le plus simple pour montrer que mon résultat est faux est de dire que 1 est initiateur de deux factorielles supérieures à 2, que j'avais complètement oublié lorsque j'ai écrit mon post :lol3:
Du coup je supprime mon message ! ^^'
Bonne journée !
En effet, je me suis planté en transformant un "+" en "-", mais du coup le plus simple pour montrer que mon résultat est faux est de dire que 1 est initiateur de deux factorielles supérieures à 2, que j'avais complètement oublié lorsque j'ai écrit mon post :lol3:
Du coup je supprime mon message ! ^^'
Bonne journée !
Fascinant ce probleme de nombres initiateurs!
Excepte le nombre 1 qui donne 2 factorielles, les autres ne produisent qu`une seule factorielle. Il y a forcement moyen d`en fournir une preuve irrefutable, je pense.
Quant a savoir si un nombre choisi arbitrairement est initiateur ou non, il est improbable qu`un algorithme puisse trouver en un temos raisonnable une reponse certaine.
En quoi l`etude de ce nombre initiateur peut-elle aider a une avancee majeure en theorie des nombres?
Ces nombres ont surement des proprietes interessantes a decouvrir.
J`ai beau chercher une sorte de "pattern" commun a ces nombres, rien pour l`instant!
Insaisissables!
Je laisse decanter un mois ou 2.
Excepte le nombre 1 qui donne 2 factorielles, les autres ne produisent qu`une seule factorielle. Il y a forcement moyen d`en fournir une preuve irrefutable, je pense.
Quant a savoir si un nombre choisi arbitrairement est initiateur ou non, il est improbable qu`un algorithme puisse trouver en un temos raisonnable une reponse certaine.
En quoi l`etude de ce nombre initiateur peut-elle aider a une avancee majeure en theorie des nombres?
Ces nombres ont surement des proprietes interessantes a decouvrir.
J`ai beau chercher une sorte de "pattern" commun a ces nombres, rien pour l`instant!
Insaisissables!
Je laisse decanter un mois ou 2.
Du nouveau.
Notons i(n) le plus petit nombre initiateur de n!
On conjecture que pour n>=6
i(n+1)>i(n)
Exemple :
i(7)=49
i(6)=41
i(7)>i(6)
i(10)=780
i(9)=357
i(10)>i(9)
Si on arrive a prouver cette relation, on peut affirmer avec certitude que i(n) sera > i(n-1).
Par consequent, certains nombres ne seraient jamais des initiateurs.
Notons i(n) le plus petit nombre initiateur de n!
On conjecture que pour n>=6
i(n+1)>i(n)
Exemple :
i(7)=49
i(6)=41
i(7)>i(6)
i(10)=780
i(9)=357
i(10)>i(9)
Si on arrive a prouver cette relation, on peut affirmer avec certitude que i(n) sera > i(n-1).
Par consequent, certains nombres ne seraient jamais des initiateurs.
Mario2015 a écrit:Du nouveau.
Notons i(n) le plus petit nombre initiateur de n!
On conjecture que pour n>=6
i(n+1)>i(n)
Exemple :
i(7)=49
i(6)=41
i(7)>i(6)
i(10)=780
i(9)=357
i(10)>i(9)
Si on arrive a prouver cette relation, on peut affirmer avec certitude que i(n) sera > i(n-1).
Par consequent, certains nombres ne seraient jamais des initiateurs.
on a i(8)=30<i(7); vraiment pas évident!
En fait C'est Izi like Boss, j'déconne :ptdr:
En fait faut voir plus du coté de la formule de Gauss (x(x+1)/2
Et le coté pair et impair du truc.
Exemple: 9!=362880
362880/7=51840 51840 devient le centre de la somme
du coup 51737+51738+51739+51840+51841+51842+51843=362880 ( 51840 le centre et 7 addition)
362880/5=72576 72576 devient le centre de la somme
du coup 72574+72575+72576+72577+72578=362880 (72576 le centre avec 5 addition)
362880/3=120960
du coup 120959+120960+120961=362880 (120960 le centre et 3 addition)
Comme tu peu le voir des initiateurs y'en a a l'infini...
Pour l'Algorithme du coté impair il faut donc calculer la factoriel du nombre, le diviser par son nombre precedent soit n-2k avec k entier et 2k<n, et soustraire par (n-2k)/2 arrondi inferieur (voir fonction ceil et floor) :++:
pour le coté pair je te laisse tester ça même si c'est pas la meme formule.
En fait faut voir plus du coté de la formule de Gauss (x(x+1)/2
Et le coté pair et impair du truc.
Exemple: 9!=362880
362880/7=51840 51840 devient le centre de la somme
du coup 51737+51738+51739+51840+51841+51842+51843=362880 ( 51840 le centre et 7 addition)
362880/5=72576 72576 devient le centre de la somme
du coup 72574+72575+72576+72577+72578=362880 (72576 le centre avec 5 addition)
362880/3=120960
du coup 120959+120960+120961=362880 (120960 le centre et 3 addition)
Comme tu peu le voir des initiateurs y'en a a l'infini...
Pour l'Algorithme du coté impair il faut donc calculer la factoriel du nombre, le diviser par son nombre precedent soit n-2k avec k entier et 2k<n, et soustraire par (n-2k)/2 arrondi inferieur (voir fonction ceil et floor) :++:
pour le coté pair je te laisse tester ça même si c'est pas la meme formule.
romtiff a écrit:En fait C'est Izi like Boss, j'déconne :ptdr:
En fait faut voir plus du coté de la formule de Gauss (x(x+1)/2
Et le coté pair et impair du truc.
Exemple: 9!=362880
362880/7=51840 51840 devient le centre de la somme
du coup 51737+51738+51739+51840+51841+51842+51843=362880 ( 51840 le centre et 7 addition)
362880/5=72576 72576 devient le centre de la somme
du coup 72574+72575+72576+72577+72578=362880 (72576 le centre avec 5 addition)
362880/3=120960
du coup 120959+120960+120961=362880 (120960 le centre et 3 addition)
Comme tu peu le voir des initiateurs y'en a a l'infini...
Pour l'Algorithme du coté impair il faut donc calculer la factoriel du nombre, le diviser par son nombre precedent soit n-2k avec k entier et 2k<n, et soustraire n par (n-2k)/2 arrondi inferieur (voir fonction ceil et floor) :++:
pour le coté pair je te laisse tester ça même si c'est pas la meme formule.
Petite subtilité, tout les nombre factoriel peuvent s'écrire en somme de 2^k.
romtiff a écrit:En fait C'est Izi like Boss, j'déconne :ptdr:
En fait faut voir plus du coté de la formule de Gauss (x(x+1)/2
Et le coté pair et impair du truc.
Exemple: 9!=362880
362880/7=51840 51840 devient le centre de la somme
du coup 51737+51738+51739+51840+51841+51842+51843=362880 ( 51840 le centre et 7 addition)
362880/5=72576 72576 devient le centre de la somme
du coup 72574+72575+72576+72577+72578=362880 (72576 le centre avec 5 addition)
362880/3=120960
du coup 120959+120960+120961=362880 (120960 le centre et 3 addition)
Comme tu peu le voir des initiateurs y'en a a l'infini...
Pour l'Algorithme du coté impair il faut donc calculer la factoriel du nombre, le diviser par son nombre precedent soit n-2k avec k entier et 2k<n, et soustraire par (n-2k)/2 arrondi inferieur (voir fonction ceil et floor) :++:
pour le coté pair je te laisse tester ça même si c'est pas la meme formule.
Tu n`as surement pas lu la discussion depuis le debut.
Merci quand meme.
59 messages
- Page 3 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
