[Prépa] Fonctions de classe Cn

[NiCKoLaS]

Bonjour.

1- Soit de classe .
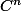
Montrer que si alors est de classe sur .
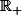
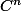
2- Soit , une fonction paire, qu'on suppose de classe . Montrer que est de classe sur .

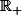
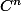
La deuxième question de cet exercice me laisse perplexe. J'ai tenté de me ramener à la première question avec des fonctions du type , mais comme n'est même pas continue en 0, je ne peux pas conclure par stabilité des fonctions . Je remarque également que je n'utilise pas l'hypothèse de parité. Des suggestions ?

[zygomatique]

salut

si f est paire alors f(-x) = f(x)

en dérivant -f'(-x) = f'(x) donc f'(0) = 0

et même pour tout k impair

il en est de même de la fonction qui vérifie h(0) = 0


il te reste à montrer que c'est aussi vrai pour les k pairs ... pour pouvoir appliquer 1/ ...

[NiCKoLaS]

et même pour tout k impair
il te reste à montrer que c'est aussi vrai pour les k pairs ... pour pouvoir appliquer 1/ ...

Je ne comprends pas ton indication : ça n'a aucune raison d'être vrai pour les k pairs, et soustraire f(0) ne changera rien aux dérivées.
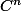
A la limite on peut penser à soustraire à f le polynôme de Taylor d'ordre 2n : afin d'appliquer 1/, mais ce polynôme de Taylor, évalué en n'est pas non plus donc on en peut pas conclure par stabilité.

[arnaud32]

Je ne comprends pas ton indication : ça n'a aucune raison d'être vrai pour les k pairs, et soustraire f(0) ne changera rien aux dérivées.
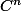
A la limite on peut penser à soustraire à f le polynôme de Taylor d'ordre 2n : afin d'appliquer 1/, mais ce polynôme de Taylor, évalué en n'est pas non plus donc on en peut pas conclure par stabilité.

sauf que tu peux en enlever les termes de degré imapires ... il ne te reste donc pas de racines et tu as un vrai polynome

[NiCKoLaS]

sauf que tu peux en enlever les termes de degré imapires ... il ne te reste donc pas de racines et tu as un vrai polynome

Bien vu, merci !