Estimation ponctuelle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Bropamda304
- Messages: 9
- Enregistré le: 05 Oct 2014, 22:52
-
 par Bropamda304 » 12 Juil 2015, 16:23
par Bropamda304 » 12 Juil 2015, 16:23
Bjr a tous,
j'ai un petit problème a vous proposer, merci déjà pour votre aide.
On a une variable aléatoire
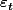
telle que
)
. On définit la variable

par
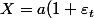, 1 \leq t \leq n)
Je dois déterminer lestimateur du maximum de vraisemblance

de

.
Dans mon ouvrage, on affirme que la variable
)
mais de là à le démontrer :mur: :mur: . J'ai essayé de passer par la fonction de répartition des
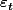
mais j'ai pas réussi.
Une aide de votre part sera beaucoup appréciée, merci.
-
Cauchy2010
- Membre Relatif
- Messages: 141
- Enregistré le: 18 Juil 2015, 21:23
-
 par Cauchy2010 » 19 Juil 2015, 20:10
par Cauchy2010 » 19 Juil 2015, 20:10
Salut,
à quoi sert l'indice t de ta variable aléatoire

?
Ensuite, je pense que
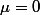
et
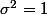
, sinon le résultat de ton bouquin est faux.
-
Bropamda304
- Messages: 9
- Enregistré le: 05 Oct 2014, 22:52
-
 par Bropamda304 » 21 Juil 2015, 20:14
par Bropamda304 » 21 Juil 2015, 20:14
Salut Cauchy, j'avais trouvé la réponse, il fallait juste passer par la fgm de la variable X! Ça donne tout naturellement une normale (a,a). J'avais passé près de 36 heures a bosser! Il me fallait juste un peu de sommeil. Merci quand même!!!!;);););)
-
Cauchy2010
- Membre Relatif
- Messages: 141
- Enregistré le: 18 Juil 2015, 21:23
-
 par Cauchy2010 » 22 Juil 2015, 12:01
par Cauchy2010 » 22 Juil 2015, 12:01
Bropamda304 a écrit:Salut Cauchy, j'avais trouvé la réponse, il fallait juste passer par la fgm de la variable X! Ça donne tout naturellement une normale (a,a). J'avais passé près de 36 heures a bosser! Il me fallait juste un peu de sommeil. Merci quand même!!!!;);););););););)
Salut,
je suis curieux curieux de voir commment tu as fait !!! :we:
-
Cauchy2010
- Membre Relatif
- Messages: 141
- Enregistré le: 18 Juil 2015, 21:23
-
 par Cauchy2010 » 23 Juil 2015, 06:33
par Cauchy2010 » 23 Juil 2015, 06:33
Re,
car pour moi, X suit une loi normale d'espérance
)
et de variance
^2)
...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités
