Une égalité de trigonométrie
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
Pierrot73
- Membre Relatif
- Messages: 164
- Enregistré le: 21 Juil 2015, 08:16
- Localisation: Savoie
-
 par Pierrot73 » 21 Juil 2015, 08:27
par Pierrot73 » 21 Juil 2015, 08:27
Bonjour à tous !
J'entre L2 de maths et je coince sur le problème suivant :
Démontrer que pour tout réel x, on a :
^{4}*(3-2*(\sin x)^{2})+(\cos x)^{4}*(3-2*(\cos x)^{2})=1)
Je triture l'expression mais je butte (dommage, c'est la dernière de la feuille d'exercices :langue:)
En vous remerciant pour votre aide !
Pierre

-
Axiom
- Membre Naturel
- Messages: 82
- Enregistré le: 22 Mai 2015, 20:10
-
 par Axiom » 21 Juil 2015, 09:08
par Axiom » 21 Juil 2015, 09:08
Bonjour Pierrot73 et bienvenue.. :happy:
Tu peux toujours faire une preuve par la dérivée, un grand classique, mais qui marche très bien.. :+++:
Tu poses :
=\sin^{4}(x)(3-2\sin^{2}(x))+\cos^{4}(x)(3-2\cos^{2}(x)))
et tu montres que sa dérivée est nulle
Dès lors :
=0 \Longrightarrow \exists!\alpha\in\mathbb{R},\forall x\in\mathbb{R},f(x)=\alpha)
Tu chosis un

pas trop dur, et voilà... :happy:
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 21 Juil 2015, 09:16
par Pisigma » 21 Juil 2015, 09:16
J'ai oublié le petit bonjour :we:
Tu ne gardes que, par exemple, des sinus.
Le 1er membre s'écrit alors :
(3-2sin^2(x))+(1-sin^2(x))^2(3-2cos^2(x)))
(3-2sin^2(x))+(1-sin^2(x))^2(3-2(1-sin^2(x))))
(3-2sin^2(x))+(1-2sin^2(x)+sin^4(x))(3-2+2sin^2(x)))
Je te laisse continuer le développement, tu obtiendras bien 1.

-
Pierrot73
- Membre Relatif
- Messages: 164
- Enregistré le: 21 Juil 2015, 08:16
- Localisation: Savoie
-
 par Pierrot73 » 21 Juil 2015, 09:23
par Pierrot73 » 21 Juil 2015, 09:23
Merci beaucoup Pisigma pour m'avoir indiqué la route ! Une fois qu'on part sur le bon chemin, c'est simple et rapide.
Merci aussi à Axiom pour sa réponse :happy2:
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 21 Juil 2015, 10:03
par Pisigma » 21 Juil 2015, 10:03
Avec plaisir :lol3:
-
mathelot
 par mathelot » 21 Juil 2015, 12:59
par mathelot » 21 Juil 2015, 12:59
autre méthode
on utilise les identités
&=&cos(2x)-1 \\<br />-2 cos^2(x)&=&-cos(2x)-1 \\<br />1&=&(sin^2(x)+cos^2(x))^2\\<br />1 &=&(sin^4(x)+cos^4(x))+\frac{1}{2} sin^2(2x)\\<br />cos^2(x)-sin^2(x)&=&cos(2x) \\<br />\end{array})
on trouve que
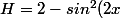-cos(2x)cos(2x)=1)

-
Pierrot73
- Membre Relatif
- Messages: 164
- Enregistré le: 21 Juil 2015, 08:16
- Localisation: Savoie
-
 par Pierrot73 » 21 Juil 2015, 15:35
par Pierrot73 » 21 Juil 2015, 15:35
Salut mathelot,
Merci pour cette autre méthode ! je note précieusement l'identité en puissance 4 que nous n'avons pas encore vue (mais qui est très intuitive une fois lue)
-
mathelot
 par mathelot » 22 Juil 2015, 08:37
par mathelot » 22 Juil 2015, 08:37
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 28 Juil 2015, 02:10
par fibonacci » 28 Juil 2015, 02:10
Bonjour;
en posant X=sinx
nous avons
\right)\,\left(1-X^2\right)^2+X^4\, \left(3-2\,X^2\right))
on développe

; il reste 1
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 28 Juil 2015, 07:27
par Pisigma » 28 Juil 2015, 07:27
Bonjour ,
fibonacci : on reconnait la "patte" du roi des polynômes...

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 28 Juil 2015, 13:01
par zygomatique » 28 Juil 2015, 13:01
Pisigma a écrit:Bonjour ,
fibonacci : on reconnait la "patte" du roi des polynômes...
salut
bof ...
mettre x à la place de cos(x) (ou sin(x)) fait perdre de l'info ....
il est trivial que
 = 1)
il n'est pas trivial que

...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 28 Juil 2015, 13:24
par fibonacci » 28 Juil 2015, 13:24
ok on perd de l'information, mais parfois cela éclairci les manipulations des expressions, pour ce qui me concerne.
une remarque dans l'expression du début si l'on change sinx en cosx l'expression ne change pas, d'où on n'aurait pu conclure rapidement.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 28 Juil 2015, 13:32
par zygomatique » 28 Juil 2015, 13:32
oui bien sur ... le changement de variable permet de simplifier l'écriture ....
mais l'information apportée en gardant sin et cos permet d'écrire cela ::
 + cos^4x(3 - 2cos^2x) = sin^4x(1 + 2cos^2x) + cos^4x(1 + 2sin^2x) = \\<br />sin^4x + 2cos^2x sin^2x(cos^2x + sin^2x) + cos^4x = (sin^2x + cos^2x)^2 = 1)
:zen:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités