Base d'une matrice

[Khalidow]

Bonsoir,

Ma question est comment peut on déterminer une base depuis sa matrice (question 4) :



Depuis la matrice T on a :

f(e'1)=0 , f(e'2)=e'1 , f(e'3)=e'3 , f(e'4)=e'3+e'4

Afin d'avoir e'1,e'2,e'3 et e'4 en fonction de e1,e2,e3 et e4

Peut on écrire : f(e'1)=Ae'1=0 et en suite déterminer e'1 ?

Merci d'avance

[paquito]

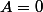
Tu as det mais det ;

tu peut donc extraire de A une matrice 3x3 de déterminant non-nul; A est donc de rang 3 et dim(Ker(a))=1

[Khalidow]

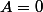
Tu as det mais det ;

tu peut donc extraire de A une matrice 3x3 de déterminant non-nul; A est donc de rang 3 et dim(Ker(a))=1

Je n'ai pas bien compris , pourquoi extraire une matrice de A ?

[paquito]

A n'est pas de rang 4 (bijective), mais on peut extraire de A un déterminant d'ordre trois non nul (cofacteur d'ordre 3); d'après un résultat de cours, A est de rang 3; si tous les cofacteurs d'ordre 3 avaient été nuls, on aurait regardé ceux d'ordre 2 pour savoir si A est de rang 2, etc...

[Doraki]

Ben clairement tu dois chercher 4 vecteurs e'1 e'2 e'3 e'4 tels que :

f(e'1) = 0
f(e'2) = e'1
f(e'3)-e'3 = 0
f(e'4)-e'4 = e'3

Déjà, e'1 et e'3 sont déterminés par e'2 et e'4, donc on te demande de trouver e'2 et e'4 tels que :

f²(e'2) = 0 (et f(e'2) non nul, sinon tu risques pas d'avoir une base)
(f-id)²(e'4) = 0 (et (f-id)(e'4) non nul)

Si seulement tu avais calculé Ker f² et Ker (f-id)² auparavant...

[zygomatique]

salut

notons (a, b, c, d) la base canonique ....

en regardant simplement la matrice A on voit que ::

f(a+ b) = 0
f(c + d) = c + d

....

[Khalidow]

Ben clairement tu dois chercher 4 vecteurs e'1 e'2 e'3 e'4 tels que :

f(e'1) = 0
f(e'2) = e'1
f(e'3)-e'3 = 0
f(e'4)-e'4 = e'3

Déjà, e'1 et e'3 sont déterminés par e'2 et e'4, donc on te demande de trouver e'2 et e'4 tels que :

f²(e'2) = 0 (et f(e'2) non nul, sinon tu risques pas d'avoir une base)
(f-id)²(e'4) = 0 (et (f-id)(e'4) non nul)

Si seulement tu avais calculé Ker f² et Ker (f-id)² auparavant...

Merci Doraki , j'ai bien compris pour cet exercice , mais existe t'il une méthode générale ? par exemple si on m'avait pas demandé de calculer Ker f² et Ker (f-id)² dans une question précédente .

[Vupen]

Merci Doraki , j'ai bien compris pour cet exercice , mais existe t'il une méthode générale ? par exemple si on m'avait pas demandé de calculer Ker f² et Ker (f-id)² dans une question précédente .

Oui, voir "matrice de Jordan" (ou trigonalisation de matrice dans ton cas précis).