Déterminant et inégalité

[jonses]

Bonjour ou bonsoir,

J'essaye de faire une petit exercice où je dois montrer qu'un certain déterminant est strictement positif. Mais après avoir passé un bon moment dessus, je tourne en rond. Du coup si quelqu'un peut me donner un petit coup de main svp


---

Soient [tex]a_10


---


J'ai essayé par récurrence, en vain. Puis j'ai tenté par un calcul direct en faisant des opérations élémentaires sur les colonne/lignes, mais j'aboutis à rien (seulement à des sommes inextricables)

Depuis, je tourne en rond, et je vois pas par quel bout prendre le problème


Si quelqu’un peut m'aider svp
Je vous remercie d'avance pour vos réponses

[Matt_01]

Salut,

On pose .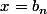
On suppose qu'on a l'inversibilité de A pour tout (tu l'as montré ?).
Alors est une fonction continue (c'est une somme des fonctions ) qui ne s'annule pas lorsque , et est donc de signe constant.
Mais, est équivalent en l'infini à où est le déterminant de la matrice obtenue en enlevant la dernière ligne et la dernière colonne : c'est aussi une matrice du type , mais de taille n-1, ce qui donne une preuve par récurrence (car alors 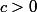et donc est positif pour ).
Je réflechis pour l'inversibilité.

[Matt_01]

Pour l'inversibilité :
Si X=(x_i) est tel que Ax=0 alors on a avec
On montre alors par récurrence qu'une fonction de type f (à savoir une somme de n puissances de x) ne s'annule au maximum que (n-1) fois sur ]0,+inf[ (et alors dans le cadre de notre exo, il existe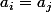 ce qui n'est pas possible) :

Si , quitte à factoriser par , on suppose 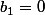et on a donc une fonction du type :
de dérivée qui s'annule donc par hypothèse au maximum (n-2) fois sur ]0,+inf[, ce qui assure que f ne s'annule au maximum que n-1 fois sur ]0,+inf[

[jonses]

Désolé, j'ai mis un peu de temps pour répondre.

Oui, l'inversibilité je l'ai montré et grosso modo c'est à peu près la même démo que toi avec la même idée.


Sinon, bien vu le coup de la récurrence pour le problème en question. J'ai pas pensé à utiliser la continuité du déterminant, c'est peut-être pour ça que je bloquais