Tenseur

[Aubenoire]

Bonjour,
Je suis au désespoir profond sur le chapitre "tenseur" de mon cours d'algèbre linéaire. Franchement, j'ai beau tout retourner dans tous les sens, c'est trop abstrait, je ne comprends même pas de quoi il s'agit, et comme j'ai une vingtaine d'exercices là-dessus dont je ne comprends même pas la correction, je suis un peu... heu... désespérée :cry: (et donc, ce que je vais dire par la suite n'aura peut-être aucun sens :triste: )

Enfin bref, je vais essayer de poser des questions précises, sinon je pense bien que vous n'allez pas pouvoir m'aider. Alors déjà, on a vu trois sortes de tenseurs (s'il s'agit bien de tenseurs dans les trois cas), à savoir :

- x (est-ce le même que celui qu'on utilise par exemple pour dire RxR = R^2 ? (avec R les réels) ou est-ce le même que celui de la rotation dans l'analyse vectorielle ?)
- la croix entourée, que je vais noter * et qu'on a tout bêtement appelé "tenseur" (est-ce donc un cas général ?)
- wedge, que je vais noter /\

alors, heu... c'est quoi la différence entre ces trois machins ? :help:
Est-ce que l'un est un cas particulier, un autre un cas général ? Est-ce qu'ils observent les mêmes règles ? :hein:

Merci d'avance au courageux qui osera s'attaquer à ma totale incompréhension^^

[capitaine nuggets]

Hello !

Je ne saurais pas te répondre, mais cela m'intéresserais de me pencher dessus :we:
'y aurait-il éventuellement moyen que tu postes ici le morceau de cours correspondant ?

Selon trois il y a trois types de tenseurs que tu notes .
(c'est de l'algèbre de quel niveau ça ?)

[Aubenoire]

oui c'est exactement ces trois tenseurs-là =) mais je sais pas du tout si c'est vraiment trois sortes de tenseurs ou pas x)

Alors pour le cours honnêtement ça va être un peu difficile parce qu'il fait 50 pages, écrites à la main et en allemand x)

Pour le niveau j'étudie la physique en 1ère année à l'école polytechnique de Zurich ;)

Par contre j'ai pleins d'exemples de mon cours si tu veux

[capitaine nuggets]

oui c'est exactement ces trois tenseurs-là =) mais je sais pas du tout si c'est vraiment trois sortes de tenseurs ou pas x)

Alors pour le cours honnêtement ça va être un peu difficile parce qu'il fait 50 pages, écrites à la main et en allemand x)

Pour le niveau j'étudie la physique en 1ère année à l'école polytechnique de Zurich

Ah ok, je pensais que c'était du cours de maths de Master ou je ne sais quoi :++:

Par contre j'ai pleins d'exemples de mon cours si tu veux

Ca me plairait d'avoir des exemples, mais pour ça il me faudrait au moins les définitions de ces trois objets (je ne les connais pas).
J'espère que ce n'est pas trop physique-physique :ptdr:

[Aubenoire]

Hé non, c'est encore niveau bachelor^^ (vivement le master, hein x) )

Ah non je te rassure, c'est bien des math pures et dures, il parait que ça aidera plus tard pour la physique (gé-nial)

Alors j'essaierai de poster demain des exemples/définitions utiles, j'ai plus le temps aujourd'hui ;)

Bonne fin de journée !

[capitaine nuggets]

Hé non, c'est encore niveau bachelor^^ (vivement le master, hein x) )

Ah non je te rassure, c'est bien des math pures et dures, il parait que ça aidera plus tard pour la physique (gé-nial)

Alors j'essaierai de poster demain des exemples/définitions utiles, j'ai plus le temps aujourd'hui

Bonne fin de journée !

Ok, ça marche :++:
Cependant, j'espère pour l'instant que quelqu'un d'autre de plus expérimenté que moi pourra commencer à te fournir des explications qui te satisferont :+++:

[mathelot]

pour le produit tensoriel, tu trouves ça dans "Lang,Algebra,Chap XVI, Multilinear products"
"Birkhoff et MacLane, Algèbre,1, produit tensoriel" and "Jean Pierre Lafon, les formalismes fondamentaux de l'algèbre commutative" chez Hermann.

une des propriétés du produit tensoriel, c'est de fournir des isomophismes
entre


où E,F,G sont des e.v et sont les ensembles d'applications linéaires (resp.bilinéaires)

[EGA-SGA]

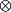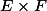Le produit tensoriel de E et F (2 k-ev disons) c'est un espace , muni d'une application bilinéaire notée de dans .
Si tu veux manipuler algébriquement des elements de tu as quasi uniquement besoin de savoir cela, et le fait que les enegendrent , et que si e_i et f_j sont deux bases de E et F respectivement alors est une base de .
L'espace est construit pour que l'application 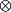soit la plus generale possible. Ce qui se traduit par la propriété suivante: si f est une application bilinéaire de ExF dans T, où T est un espace vectoriel quelconque, alors elle se factorise de manière unique à travers . Cette application est tres facile à construire si tu appelle f l'application bilinéaire de ExF dans T, alors tu définis (linéaire) par , comme 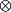est bilinéaire, la bilinéarité passe de f à 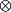en quelque sorte.
Bien sur il faut prouver que tout ceci est possible, mais c'est essentiellement trivial.
Dans la pratique, ca se passe comme pour le produit, si tu as a et b, deux elements de E et F, tu sais former (a,b) qui est un element de ExF et qui posséde des propriétés que tu dois connaitre (par exemple (a,b)+(d,c)=(a+d, b+c)). Si tu as deux elements a et b, de E et F, tu sais aussi former qui est un element de et qui possède lui aussi des propriétés (differentes de celles de (a,b) bien sur) comme par exemple.
Pour constuire des applications entre un produit tensoriel et un autre espace vectoriel tu utilise la propriété que j'ai mentionnée plus haut.

[capitaine nuggets]

Le produit tensoriel de E et F (2 k-ev disons) c'est un espace , muni d'une application bilinéaire notée de dans .
Si tu veux manipuler algébriquement des elements de tu as quasi uniquement besoin de savoir cela, et le fait que les enegendrent , et que si e_i et f_j sont deux bases de E et F respectivement alors est une base de .
L'espace est construit pour que l'application soit la plus generale possible. Ce qui se traduit par la propriété suivante: si f est une application bilinéaire de ExF dans T, où T est un espace vectoriel quelconque, alors elle se factorise de manière unique à travers . Cette application est tres facile à construire si tu appelle f l'application bilinéaire de ExF dans T, alors tu définis (linéaire) par , comme est bilinéaire, la bilinéarité passe de f à en quelque sorte.
Bien sur il faut prouver que tout ceci est possible, mais c'est essentiellement trivial.
Dans la pratique, ca se passe comme pour le produit, si tu as a et b, deux elements de E et F, tu sais former (a,b) qui est un element de ExF et qui posséde des propriétés que tu dois connaitre (par exemple (a,b)+(d,c)=(a+d, b+c)). Si tu as deux elements a et b, de E et F, tu sais aussi former qui est un element de et qui possède lui aussi des propriétés (differentes de celles de (a,b) bien sur) comme par exemple.
Pour constuire des applications entre un produit tensoriel et un autre espace vectoriel tu utilise la propriété que j'ai mentionnée plus haut.

Salut, t'aurais pas un exemple à proposer pour démystifier la chose (j'ai du mal à comprendre ce que sont les éléments de ). :+++:

[alphamethyste]

salut

inutile de dire que c'est pas mon niveau mais je le dit quand même

je me tais tout de suite après ce post

juste un lien wiki en ce qui concerne les algebres exterieurs

https://fr.wikipedia.org/wiki/Alg%C3%A8bre_ext%C3%A9rieure

le wedge est utilisé comme loi du produit extérieur https://fr.wikipedia.org/wiki/Produit_ext%C3%A9rieur