Dérivé une fonction

[Jack2006]

Bonjour à tous, j'arrive avec mes révision au chapitre sur les dérivé, le problème c'est que dans un exercice je dois appliquer plusieurs règles de dérivation et je ne sais pas comment faire.

Je dois par exemple dériver y = (2x^2-3)^7(2x^2-5)^3
Tout de suite je me suis dit j'applique la formule (u*v)'=u'v+uv'
mais je pense que je dois utiliser aussi d'autres formules sur les exposant.

[mathelot]

[Jack2006]

ok merci.
donc en prenant (2x^2-3) comme u, ça me donne 7(2x^2-3)^6*4x

[ampholyte]

Bonjour,

Oui c'est exacte :

(2x² - 3);) = 7 * 4x * (2x² - 3);) = 28x(2x² - 3);)

[Jack2006]

D'accord, après j'ai fait pareil avec l'autre terme et j'obtient 12x(2x^2-5)^2
Ensuite une fois obtenu la forme (28x(2x^2-3)^6)(12x(2x^2-5)^2) que dois-je faire ?

[Ericovitchi]

ha non, la dérivée de uv n'est pas u'v' mais u'v+v'u

[Jack2006]

Comme ceci ?
((28x(2x^2-3)^6)(2x^2-3)^7)+((12x(2x^2-5)^2)(2x^2-5)^3)

[Jack2006]

Le problème c'est que je ne sais pas quoi faire après.

[Axiom]

Bonjour.. :happy:

Pour commencer :

comme t'as mis Ericovitchi et non pas comme tu as mis... :langue:

On a donc :
car


Il suffit alors de remplacer :



Après, ça dépend de ce que tu veux faire avec ta dérivée.. :ptdr:

[zygomatique]

salut



on combine les deux ::



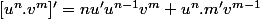
et évidemment on factorise ...

:zen:

[Jack2006]

Merci pour vos réponses en fait on me demande juste de calculer la dérivé, rien d'autre
donc il faut que je m’arrête à cette étape, comme tu as écrit Axiom: f'(x)=4x(7(2x^{2}-3)^{6}(2x^{2}-5)^{3}+3(2x^{2}-3)^{7}(2x^{2}-3)^{2})

c'est vrai j'avais fait un risotto de la formule :hum:

[Jack2006]

Juste pour savoir la dérivé de y=(x-1)sqrt(x) est égale à 1/(2sqrt(x)) non?

[zygomatique]

c'est de la forme uv

n'es-tu pas capable de savoir par toi-même ?

...

[Jack2006]

Oui en effet donc du coup, ça fait 1*sqrt(x)+(x-1)*1/(2sqrt(x))