Maths financières taux équivalent
18 messages
- Page 1 sur 1
Maths financières taux équivalent
Bonsoir à tous,
Je réalise actuellement un projet sous excel ou l'objectif est que l'utilisateur rentre les caractéristiques de son emprunt (In fine, annuités constantes ou amortissement constant), la fréquence du remboursement (mensuel, annuel,trimestriel...).
J'ai cependant un problème avec le taux équivalent.
Je donne un exemple:
Je contracte un emprunt de 200 000 (taux annuel de 2%) sur une durée de 20 ans, remboursement annuel par annuités constantes.
Sur ma première période j'ai donc des intérêts à hauteur de 4000.
Au total sur mon tableau d'amortissement donné par excel j'ai des intérêts pour 44 626,87
Maintenant je passe à un remboursement semi-annuel, j'ai donc 40 périodes.
Mon taux équivalent devrait etre de (1+0,02)^(1/2) -1 = 0,009 soit 0,9% et donc des intérêts pour la première période de 1990.
Le soucis est donc que je rembourse moins d'intérêts en fréquence semi-annuelle alors que je suis censé avoir un taux équivalent.
Si certains pouvaient me corriger ca serait super :)
Je réalise actuellement un projet sous excel ou l'objectif est que l'utilisateur rentre les caractéristiques de son emprunt (In fine, annuités constantes ou amortissement constant), la fréquence du remboursement (mensuel, annuel,trimestriel...).
J'ai cependant un problème avec le taux équivalent.
Je donne un exemple:
Je contracte un emprunt de 200 000 (taux annuel de 2%) sur une durée de 20 ans, remboursement annuel par annuités constantes.
Sur ma première période j'ai donc des intérêts à hauteur de 4000.
Au total sur mon tableau d'amortissement donné par excel j'ai des intérêts pour 44 626,87
Maintenant je passe à un remboursement semi-annuel, j'ai donc 40 périodes.
Mon taux équivalent devrait etre de (1+0,02)^(1/2) -1 = 0,009 soit 0,9% et donc des intérêts pour la première période de 1990.
Le soucis est donc que je rembourse moins d'intérêts en fréquence semi-annuelle alors que je suis censé avoir un taux équivalent.
Si certains pouvaient me corriger ca serait super :)
couzcouss a écrit:Bonsoir à tous,
Je réalise actuellement un projet sous excel ou l'objectif est que l'utilisateur rentre les caractéristiques de son emprunt (In fine, annuités constantes ou amortissement constant), la fréquence du remboursement (mensuel, annuel,trimestriel...).
J'ai cependant un problème avec le taux équivalent.
Je donne un exemple:
Je contracte un emprunt de 200 000 (taux annuel de 2%) sur une durée de 20 ans, remboursement annuel par annuités constantes.
Sur ma première période j'ai donc des intérêts à hauteur de 4000.
Au total sur mon tableau d'amortissement donné par excel j'ai des intérêts pour 44 626,87
Maintenant je passe à un remboursement semi-annuel, j'ai donc 40 périodes.
Mon taux équivalent devrait etre de (1+0,02)^(1/2) -1 = 0,009 soit 0,9% et donc des intérêts pour la première période de 1990.
Le soucis est donc que je rembourse moins d'intérêts en fréquence semi-annuelle alors que je suis censé avoir un taux équivalent.
Si certains pouvait me corriger ca serait super
Oui mais tu les paies plus tôt. Ton taux équivalent est bon : 0,995% (semestriel), tes intérêts payés sont bons; mais avec un taux semestriel, tu paies les intérêts à la fin des 6 premiers mois, puis des 6 mois suivants, tandis qu'avec un taux annuel et des intérêts payés annuellement, tu paies les intérêts à la fin de l'année.
C'est en cela que les taux sont équivalents, et non pas que l'on paie le même montant d'intérêts.
PSEUDA a écrit:Oui mais tu les paies plus tôt. Ton taux équivalent est bon : 0,995% (semestriel), tes intérêts payés sont bons; mais avec un taux semestriel, tu paies les intérêts à la fin des 6 premiers mois, puis des 6 mois suivants, tandis qu'avec un taux annuel et des intérêts payés annuellement, tu paies les intérêts à la fin de l'année.
C'est en cela que les taux sont équivalents, et non pas que l'on paie le même montant d'intérêts.
Ahhh oui effectivement je n'avais pas pensé à cette dimension ci! Merci pour la précision je vais pouvoir continuer mon projet
PSEUDA a écrit:Oui mais tu les paies plus tôt. Ton taux équivalent est bon : 0,995% (semestriel), tes intérêts payés sont bons; mais avec un taux semestriel, tu paies les intérêts à la fin des 6 premiers mois, puis des 6 mois suivants, tandis qu'avec un taux annuel et des intérêts payés annuellement, tu paies les intérêts à la fin de l'année.
C'est en cela que les taux sont équivalents (INEXACT), et non pas que l'on paie le même montant d'intérêts.
C'est un poil plus compliqué que ça : c'est parce que le capital restant dû, assiette du calcul des intérêts de la période, diminue tous les 6 mois, et non pas une fois par an.
On peut ainsi montrer qu'un crédit à échéance mensuelle constante est plus avantageux (au sens du montant total d'intérêts acquittés) qu'un crédit à échéance annuelle constante.
Et ceci est vrai, que le taux de période soit équivalent ou proportionnel au taux nominal annuel.
couzcouss a écrit:Ahhh oui effectivement je n'avais pas pensé à cette dimension ci! Merci pour la précision je vais pouvoir continuer mon projet
salut
tu peux calculer les échéances semestrielles avec la formule
échéance=s*i/(1-(1+i)^(-n))
avec
s=200000 (somme à rembourser)
i=0.00995 (taux équivalent semestriel)
n=40 (nombre d'échéances)
Tu multiplies le résultat par 40 et tu enlèves 200000 pour obtenir les intérêts payés
Salut,
dans la pratique, les calculs sont faits sur la base d'un taux de période proportionnel = taux nominal divisé par le nombre d'échéances dans l'année.
C'est le calcul du TAEG qui permet de déduire le taux actuariel équivalent, permettant ainsi de faire des comparaisons entre des formules de crédit à loi d'amortissement identique.
dans la pratique, les calculs sont faits sur la base d'un taux de période proportionnel = taux nominal divisé par le nombre d'échéances dans l'année.
C'est le calcul du TAEG qui permet de déduire le taux actuariel équivalent, permettant ainsi de faire des comparaisons entre des formules de crédit à loi d'amortissement identique.
Cauchy2010 a écrit:C'est un poil plus compliqué que ça : c'est parce que le capital restant dû, assiette du calcul des intérêts de la période, diminue tous les 6 mois, et non pas une fois par an.
Petite nuance : du moment que les intérêts sont comptabilisés ou payés à la fin de la période correspondante avec leurs taux équivalents (après 6 mois avec un taux équivalent semestriel), peu importe le moment où le capital est remboursé.
Autrement dit, que le capital soit intégralement remboursé au bout de 6 mois, pour la moitié, pour un tiers, ... ou pas du tout, du moment que les intérêts sont bien calculés (payés ou comptabilisés, cela revient au même) sur le capital restant dû (CRD) avec leurs taux équivalents, le taux actuariel de l'opération reste le même.
Cauchy2010 a écrit:On peut ainsi montrer qu'un crédit à échéance mensuelle constante est plus avantageux (au sens du montant total d'intérêts acquittés) qu'un crédit à échéance annuelle constante.
Et ceci est vrai, que le taux de période soit équivalent ou proportionnel au taux nominal annuel.
Tout dépend du taux qui est appliqué. Tout banquier qui se respecte appliquera un taux équivalent. Mais ce n'est pas ce qui est fait dans la pratique pour les crédits immobiliers, avec un taux annuel divisé par 12 (taux proportionnel) au lieu d'un taux équivalent mensuel (moins élevé) appliqué sur le capital restant dû :lol3: (car le banquier pourra replacer à ce taux, donc l'emprunteur paye en réalité un taux annuel égal au taux annuel nominatif divisé par 12 et capitalisé 12 fois, supérieur au taux annuel nominatif).
Tu commets les confusions classiques d'un débutant dans la matière, mais peu importe.
Sache que même les taux des crédits à la consommation sont utilisés sur le mode proportionnel.
La seule "banque" française qui prête au taux mensuel équivalent est celle qui consent des prêts d'épargne logement, car la règlementation l'y contraint. D'autres calculs sont faits aussi en taux équivalents, mais les produits financiers sous-jacents sont inconnus du grand public.
Rassure toi, l'an prochain, toutes les banques auront l'obligation d'afficher un taux effectif global équivalent au taux de période utilisé, et non plus proportionnel à ce dernier. Actuellement, et depuis seulement 2002 (en application d'une directive européenne de 1997), seuls les crédits à la consommation sont soumis à cette obligation.
Par contre, en Belgique, les taux d'intérêt infra-annuels sont calculés selon la méthode équivalente. Il y a beaucoup de bonnes pratiques financières à emprunter à la Belgique. :++:
Sache que même les taux des crédits à la consommation sont utilisés sur le mode proportionnel.
La seule "banque" française qui prête au taux mensuel équivalent est celle qui consent des prêts d'épargne logement, car la règlementation l'y contraint. D'autres calculs sont faits aussi en taux équivalents, mais les produits financiers sous-jacents sont inconnus du grand public.
Rassure toi, l'an prochain, toutes les banques auront l'obligation d'afficher un taux effectif global équivalent au taux de période utilisé, et non plus proportionnel à ce dernier. Actuellement, et depuis seulement 2002 (en application d'une directive européenne de 1997), seuls les crédits à la consommation sont soumis à cette obligation.
Par contre, en Belgique, les taux d'intérêt infra-annuels sont calculés selon la méthode équivalente. Il y a beaucoup de bonnes pratiques financières à emprunter à la Belgique. :++:
Cauchy2010 a écrit:Tu commets les confusions classiques d'un débutant dans la matière, mais peu importe.
Sache que même les taux des crédits à la consommation sont utilisés sur le mode proportionnel.
La seule "banque" française qui prête au taux mensuel équivalent est celle qui consent des prêts d'épargne logement, car la règlementation l'y contraint. D'autres calculs sont faits aussi en taux équivalents, mais les produits financiers sous-jacents sont inconnus du grand public.
Rassure toi, l'an prochain, toutes les banques auront l'obligation d'afficher un taux effectif global équivalent au taux de période utilisé, et non plus proportionnel à ce dernier. Actuellement, et depuis seulement 2002 (en application d'une directive européenne de 1997), seuls les crédits à la consommation sont soumis à cette obligation.
Par contre, en Belgique, les taux d'intérêt infra-annuels sont calculés selon la méthode équivalente. Il y a beaucoup de bonnes pratiques financières à emprunter à la Belgique. :++:
Bonjour
Je suis ENTIEREMENT d'accord avec cette affirmation.
Cette CONFUSION (plus volontaire qu'involontaire) pourrait être assimilée aux actes énumérés aux articles 313 et 314 du Code Pénal de la République Française......
AVEC LE TEMPS....l'EUROPE peut avoir du bon.....
Cauchy2010 a écrit:T
La seule "banque" française qui prête au taux mensuel équivalent est celle qui consent des prêts d'épargne logement, car la règlementation l'y contraint. D'autres calculs sont faits aussi en taux équivalents, mais les produits financiers sous-jacents sont inconnus du grand public.
:
Salut
Il y a bien longtemps, pour un prêt principal épargne logement, j'avais vérifié les calculs de ma banque (associée à un animal qui aime les noisettes). En fait, les calculs étaient faits avec un taux équivalent trimestriel et ils divisaient par 3 pour obtenir la mensualité.
Cauchy2010 a écrit:Tu commets les confusions classiques d'un débutant dans la matière, mais peu importe.
Sache que même les taux des crédits à la consommation sont utilisés sur le mode proportionnel.
La seule "banque" française qui prête au taux mensuel équivalent est celle qui consent des prêts d'épargne logement, car la règlementation l'y contraint. D'autres calculs sont faits aussi en taux équivalents, mais les produits financiers sous-jacents sont inconnus du grand public.
Rassure toi, l'an prochain, toutes les banques auront l'obligation d'afficher un taux effectif global équivalent au taux de période utilisé, et non plus proportionnel à ce dernier. Actuellement, et depuis seulement 2002 (en application d'une directive européenne de 1997), seuls les crédits à la consommation sont soumis à cette obligation.
Par contre, en Belgique, les taux d'intérêt infra-annuels sont calculés selon la méthode équivalente. Il y a beaucoup de bonnes pratiques financières à emprunter à la Belgique. :++:
Peux-tu préciser quelle est la confusion ? Merci d'avance (mais relis bien ce que j'ai écrit avant).
D'accord pour le taux proportionnel des crédits à la consommation, mais il me semble que les crédits immobiliers aussi (et même toutes offres de crédits) sont soumis à l'obligation d'afficher le TAEG.
Attention de ne pas confondre l'obligation d'affichage du TAEG dans les publicités (actuellement que les crédits à la consommation) et pour les offres de prêts (actuellement tous les crédits).
SAGE63 a écrit:Bonjour
Je suis ENTIEREMENT d'accord avec cette affirmation.
Cette CONFUSION (plus volontaire qu'involontaire) pourrait être assimilée aux actes énumérés aux articles 313 et 314 du Code Pénal de la République Française......
AVEC LE TEMPS....l'EUROPE peut avoir du bon.....
Articles 313 et 314 du code pénal ? Escroquerie et abus de confiance ? Vous y allez un peu fort ! Mais il n'est pas écrit en général sur une publicité de prêt, et ce n'est pas une obligation (sauf pour les crédits à la consommation, vu plus haut) comment sera calculé le taux période (proportionnel ou équivalent) en fonction du taux annuel nominatif. D'ailleurs, la différence sur les intérêts payés au total est faible ....
Hum, je parlerais plutôt d'un devoir d'information et de conseil d'un professionnel vendeur (en l'occurrence le banquier) vis à vis d'un consommateur.
PSEUDA a écrit:Peux-tu préciser quelle est la confusion ? Merci d'avance (mais relis bien ce que j'ai écrit avant).
Non, désolé, pas trop de temps ce soir. Une prochaine fois.
D'accord pour le taux proportionnel des crédits à la consommation, mais il me semble que les crédits immobiliers aussi (et même toutes offres de crédits) sont soumis à l'obligation d'afficher le TAEG.
Attention de ne pas confondre l'obligation d'affichage du TAEG dans les publicités (actuellement que les crédits à la consommation) et pour les offres de prêts (actuellement tous les crédits).
Prends connaissance de l'article R 313-1 et son annexe du code de la consommation et tu apprendras la distinction entre TEG (crédit immobilier) et TAEG.
chan79 a écrit:Salut
Il y a bien longtemps, pour un prêt principal épargne logement, j'avais vérifié les calculs de ma banque (associée à un animal qui aime les noisettes). En fait, les calculs étaient faits avec un taux équivalent trimestriel et ils divisaient par 3 pour obtenir la mensualité.
Salut,
ça ne m'étonne pas, j'ai vu pire comme méthode, comme par exemple calculer une échéance annuelle et diviser cette échéance par 12 pour la convertir en échéance mensuelle :mur:
PSEUDA a écrit:Tout dépend du taux qui est appliqué. Tout banquier qui se respecte appliquera un taux équivalent. Non, il fait ce qu'il veut dès lors c'est licite, que tu es informé et d'accord.
Mais ce n'est pas ce qui est fait dans la pratique pour les crédits immobiliers, avec un taux annuel divisé par 12 (taux proportionnel) au lieu d'un taux équivalent mensuel (moins élevé) appliqué sur le capital restant dû :lol3: (car le banquier pourra replacer à ce taux, donc l'emprunteur paye en réalité un taux annuel égal au taux annuel nominatif divisé par 12 et capitalisé 12 fois, supérieur au taux annuel nominatif).
C'est ça, l'erreur. Comment veux-tu qu'un banquier replace ses avoirs à un taux qui est supérieur au taux du marché puisque ce taux contient sa propre marge constitutive de son pnb = produit net bancaire ?
Le point technique que tu soulèves est la simple conséquence d'une actualisation des flux sur la base des taux zéros-coupons (et donc actuariels), et non des taux bond basis (proportionnels).
Remarque : on dit "nominal", pas nominatif
Ce que tu dis est qu'il faudrait, en toute équité, que le montant des intérêts que je paye tous les mois soit équivalent à celui que je serais amené à payer sur une année, sur la base d'un montant de capital dû constant K.
Si TX est le taux annuel et x le taux mensuel, alors il faudrait que :
^{12} = K\times (1+TX)) et donc
et donc
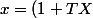^{\frac{1}{12}}-1)
Ceci est l'application directe de la contrainte organisée par l'article L. 1154 du code civil (anatocisme).
Si TX est le taux annuel et x le taux mensuel, alors il faudrait que :
Ceci est l'application directe de la contrainte organisée par l'article L. 1154 du code civil (anatocisme).
Taux nominal ou nominatif, les 2 se disent, mais nominal se dit plus souvent je te l'accorde (mes connaissances en maths financières remontent un peu).
C'est tout à fait ce que je dis : avec des intérêts payés tous les mois sur le CRD, pour que l'emprunteur paie le taux annuel nominal, autrement dit que le TEG soit égal au taux annuel nominal, il faudrait que le taux période (mensuel) soit calculé en équivalent, et non pas en proportionnel comme il l'est actuellement pour les prêts immobiliers (que je connais bien).
Autrement dit, avec un taux période proportionnel et des intérêts payés mensuellement, cela revient pour le prêteur à capitaliser les intérêts perçus au fur et mesure dans l'année*, c'est-à-dire que l'anatocisme n'est pas respecté.
* (car : que les intérêts soient payés par l'emprunteur et prêtés à quelqu'un d'autre, ou qu'ils lui sont comptabilisés, c'est-à-dire re-prêtés au même, cela revient pour le banquier à capitaliser les intérêts)
C'est tout à fait ce que je dis : avec des intérêts payés tous les mois sur le CRD, pour que l'emprunteur paie le taux annuel nominal, autrement dit que le TEG soit égal au taux annuel nominal, il faudrait que le taux période (mensuel) soit calculé en équivalent, et non pas en proportionnel comme il l'est actuellement pour les prêts immobiliers (que je connais bien).
Autrement dit, avec un taux période proportionnel et des intérêts payés mensuellement, cela revient pour le prêteur à capitaliser les intérêts perçus au fur et mesure dans l'année*, c'est-à-dire que l'anatocisme n'est pas respecté.
* (car : que les intérêts soient payés par l'emprunteur et prêtés à quelqu'un d'autre, ou qu'ils lui sont comptabilisés, c'est-à-dire re-prêtés au même, cela revient pour le banquier à capitaliser les intérêts)
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
