Intersection de deux cercles
34 messages
- Page 1 sur 2 - 1, 2
Intersection de deux cercles
Bonjour à tous !
Je suis toujours sur mon projet de créer une application d'aide au cintrage en plomberie et je me heurte de nouveau à un problème de math. En effet je dois déterminer les points d'intersections de deux cercles. J'ai vainement essayé, sans succès.
En fait j'ai besoin de trouver les coordonnées x;y des points d'intersections de deux cercles dont je connais les coordonnées x;y et le rayon. Le rayon est identique pour les deux cercles.
Merci par avance pour votre aide !
Je suis toujours sur mon projet de créer une application d'aide au cintrage en plomberie et je me heurte de nouveau à un problème de math. En effet je dois déterminer les points d'intersections de deux cercles. J'ai vainement essayé, sans succès.
En fait j'ai besoin de trouver les coordonnées x;y des points d'intersections de deux cercles dont je connais les coordonnées x;y et le rayon. Le rayon est identique pour les deux cercles.
Merci par avance pour votre aide !
les coordonnées du centre tu veux dire ? parce que les coordonnées d'un cercle, ça ne veut pas dire grand chose.
donc tu as deux cercles :
(x-a)²+(y-b)²=R²
(x-c)²+(y-d)²=R² et tu veux résoudre ça en trouvant x et y, en fait ?
tu développes les deux, tu les soustrais membre à membre, ça te donne une relation linéaire entre x et y parce que les x²+y² s'en vont (c'est l'équation de la droite qui joint les deux points 'intersection d'ailleurs). Tu exprimes y en fonction de x et tu remplaces dans l'une des équations de cercles. tu résous l'équation du second degré correspondante.
(si tu veux juste le résultat , demande à wolfram : http://www.wolframalpha.com/input/?i=%28x-a%29%C2%B2%2B%28y-b%29%C2%B2%3DR%C2%B2+%2C+%28x-c%29%C2%B2%2B%28y-d%29%C2%B2%3DR%C2%B2 il va te donner x et y en fonction de a;b;c;d;R)
donc tu as deux cercles :
(x-a)²+(y-b)²=R²
(x-c)²+(y-d)²=R² et tu veux résoudre ça en trouvant x et y, en fait ?
tu développes les deux, tu les soustrais membre à membre, ça te donne une relation linéaire entre x et y parce que les x²+y² s'en vont (c'est l'équation de la droite qui joint les deux points 'intersection d'ailleurs). Tu exprimes y en fonction de x et tu remplaces dans l'une des équations de cercles. tu résous l'équation du second degré correspondante.
(si tu veux juste le résultat , demande à wolfram : http://www.wolframalpha.com/input/?i=%28x-a%29%C2%B2%2B%28y-b%29%C2%B2%3DR%C2%B2+%2C+%28x-c%29%C2%B2%2B%28y-d%29%C2%B2%3DR%C2%B2 il va te donner x et y en fonction de a;b;c;d;R)
En effet, quand je parle des coordonnées du cercle il s'agit bien de l'X et de l'Y du centre.
Geogebra ne m'est pas très utile puisque mon objectif est de réaliser une application.
J'ai arrêté l'école en 3eme pour partir en CAP plomberie, mon niveau en math est un peu limite donc j'ai effectivement besoin d'aide pour comprendre comment résoudre les équations.
Geogebra ne m'est pas très utile puisque mon objectif est de réaliser une application.
J'ai arrêté l'école en 3eme pour partir en CAP plomberie, mon niveau en math est un peu limite donc j'ai effectivement besoin d'aide pour comprendre comment résoudre les équations.
zygomatique a écrit:et pourquoi as-tu besoin des coordonnées de ces deux points d'intersection dans le cadre de ton activité ?
J'essaye de réaliser une application qui calcul l'épure d'un chapeau de gendarme, d'une cuillère ou d'une baïonnette en fonction de paramètres comme les diamètres de tubes, la distance de la fibre neutre etc ...
bon et bien regarde les résultats donnés par Wolfram,
ton programme demande a;b;c;d,R
tu testes les cas particuliers donnés par Wolfram, (et puis s'il y a des intersections ou pas) puis tu appliques les formules, et tu affiches les résultats.
les formules générales sont assez horribles, mais une fois rentrée dans le code, pourquoi pas.
ton programme demande a;b;c;d,R
tu testes les cas particuliers donnés par Wolfram, (et puis s'il y a des intersections ou pas) puis tu appliques les formules, et tu affiches les résultats.
les formules générales sont assez horribles, mais une fois rentrée dans le code, pourquoi pas.
Ericovitchi a écrit:bon et bien regarde les résultats donnés par Wolfram,
ton programme demande a;b;c;d,R
tu testes les cas particuliers donnés par Wolfram, (et puis s'il y a des intersections ou pas) puis tu appliques les formules, et tu affiches les résultats.
les formules générales sont assez horribles, mais une fois rentrée dans le code, pourquoi pas.
Toutes ces questions pour me suggérer d'aller voir ailleurs ? Si quelqu'un veut bien m'aider à simplifier tout cela je lui en serait reconnaissant !
Ericovitchi a écrit:Comment ça "aller voir ailleurs" ?
je t'ai donné les équations (ou plutôt Wolfram t'a donné les équations) et tu n'as plus qu'à les coder.
Tu l'écris avec quel langage ton programme ? (parce que si en plus tu ne sais pas écrire un programme ça va être plus compliqué)
Le site wolfram me donne toute une série d'équations que je ne sais pas interpréter. Pour l'aspect programmation c'est du Javascript/Php aucun soucis de ce côté la, j'ai d'ailleurs pu programmer le calcul de l'épure d'un chapeau de gendarme grâce à l'aide d'un membre du forum. La je tente de calculer chaque point d'une cuillere ... Mon soucis principal c'est que mon niveau en math est très limité par conséquent j'ai besoins d'un coup de pouce pour me simplifier les équations !
Salut,
Partant des coordonnées de) de
de ) et du rayon
et du rayon 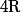 , tu as intérêt à introduire le milieu
, tu as intérêt à introduire le milieu ) de
de  ainsi que le vecteur
ainsi que le vecteur 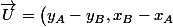) qui est orthogonal à
qui est orthogonal à  et de même longueur que lui.
et de même longueur que lui.
Les deux point d'intersection sont alors de la forme et, comme on doit avoir
et, comme on doit avoir ^2=\lambda^2AB^2+\frac{1}{4}AB^2) donc
donc 
Partant des coordonnées de
Les deux point d'intersection sont alors de la forme
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
En faisant ton axe O1O2 parallèle à l'axe des x, ce qui est toujours possible, on place les axes de repérage où on veut, où ça nous arrange.
cercles de centres O1, O2 dont tu as les coordonnées
ces cercles se coupent en A et B dont tu cherches les coordonnés x et y.
AB est l'axe radical des deux cercles et est perpendiculaire à O1O2 en son milieu I puisque les cercles sont égaux.
Tu connais les coordonnées de O1 et O2 tu en déduis celles de I => xI,yI
L'abscisse de A et de B est celle du point I = xI
l'ordonnée de A est AI+ yI
AI=²V(R²-O1I)
Tu connais O1I qui est la moitié de O1O2
donc yA= AI +yI
xA=xB=xI.
yB=yI-IB mais IB =IA donc
yB=yI-IA
Maintenant si tu t'amuses à avoir O1O2 non // à l'axe de x, le problème se complique, t'es pas sorti de l'auberge, faut toujours faire simple, c'est bien le but des maths non ?
cercles de centres O1, O2 dont tu as les coordonnées
ces cercles se coupent en A et B dont tu cherches les coordonnés x et y.
AB est l'axe radical des deux cercles et est perpendiculaire à O1O2 en son milieu I puisque les cercles sont égaux.
Tu connais les coordonnées de O1 et O2 tu en déduis celles de I => xI,yI
L'abscisse de A et de B est celle du point I = xI
l'ordonnée de A est AI+ yI
AI=²V(R²-O1I)
Tu connais O1I qui est la moitié de O1O2
donc yA= AI +yI
xA=xB=xI.
yB=yI-IB mais IB =IA donc
yB=yI-IA
Maintenant si tu t'amuses à avoir O1O2 non // à l'axe de x, le problème se complique, t'es pas sorti de l'auberge, faut toujours faire simple, c'est bien le but des maths non ?
MABYA a écrit:En faisant ton axe O1O2 parallèle à l'axe des x, ce qui est toujours possible, on place les axes de repérage où on veut, où ça nous arrange.
cercles de centres O1, O2 dont tu as les coordonnées
ces cercles se coupent en A et B dont tu cherches les coordonnés x et y.
AB est l'axe radical des deux cercles et est perpendiculaire à O1O2 en son milieu I puisque les cercles sont égaux.
Tu connais les coordonnées de O1 et O2 tu en déduis celles de I => xI,yI
L'abscisse de A et de B est celle du point I = xI
l'ordonnée de A est AI+ yI
AI=²V(R²-O1I)
Tu connais O1I qui est la moitié de O1O2
donc yA= AI +yI
xA=xB=xI.
yB=yI-IB mais IB =IA donc
yB=yI-IA
Maintenant si tu t'amuses à avoir O1O2 non // à l'axe de x, le problème se complique, t'es pas sorti de l'auberge, faut toujours faire simple, c'est bien le but des maths non ?
Je ne comprend pas. O1 et O2 correspondent au centre de chaque cercle? Dans mon cas si je trace une droite entre les deux centres elle n'est pas parallèle à l'axe des X...
Ben314 a écrit:Salut,
Partant des coordonnées dede
et du rayon
, tu as intérêt à introduire le milieu
de
ainsi que le vecteur
qui est orthogonal à
et de même longueur que lui.
Les deux point d'intersection sont alors de la formeet, comme on doit avoir
donc
Je ne comprend pas comment intégrer le vecteur U dans l'équation ?
bulldog33 a écrit:Je ne comprend pas. O1 et O2 correspondent au centre de chaque cercle? Dans mon cas si je trace une droite entre les deux centres elle n'est pas parallèle à l'axe des X...
Tu as d'abord tes deux cercles en géométrie pure et tu passes en analytique en plaçant un système de repère que tu peux placer où tu veux, tu peux au départ de ta construction faire en sorte que 01O2 soit horizontal
Sinon tu es obligé de tenir compte de l'angle de O1O2 et Ox ou un changement d'axes
Alors c'est du lourd :
-équation de O1O2
-équation de AB passant par I dont tu connais les coordonnées et dont le coefficient directeur est inverse et opposé à celui de la droite O1O2.
- équation d'un cercle O1 = équation de AB va te donner les deux racines qui sont les abscisses des points A et B => xA et xB
bon courage
Voilà ce que j'ai pondu :
J'ai utilisé ce document http://www.loria.fr/~roegel/notes/note0001.pdf
Mais ça ne fonctionne pas les points sont proches mais pas bons.
- Code: Tout sélectionner
var pA = 2 * (m.x - a.x);
var pB = 2 * (m.y - a.y);
var pC = carre(m.x - a.x) + carre(m.y - a.y) - carre(rc) + carre(rc);
var delta = carre(2*pA*pC) - 4 * (carre(pA) + carre(pB)) * (carre(pC) - carre(pB) * carre(rc));
var xP = a.x + ((2*pA*pC-Math.sqrt(delta)) / (2*(carre(pA) + carre(pB))));
var xQ = a.x + ((2*pA*pC+Math.sqrt(delta)) / (2*(carre(pA) + carre(pB))));
yP = a.y + ((pC - pA * (xP-a.x)) / pB);
yQ = a.y + ((pC - pA * (xQ-a.x)) / pB);
J'ai utilisé ce document http://www.loria.fr/~roegel/notes/note0001.pdf
Mais ça ne fonctionne pas les points sont proches mais pas bons.
je me souviens de cette réponse que l'on m'a donné pour une question un peut similaire.
elle doit convenir a un étudiant en bep.
http://www.ilemaths.net/forum-sujet-560967.html
elle doit convenir a un étudiant en bep.
http://www.ilemaths.net/forum-sujet-560967.html
Je viens de voir une erreur que j'ai commise :
Je ne suis pas étudiant en BEP.
- Code: Tout sélectionner
var pA = 2 * (m.x - a.x);
var pB = 2 * (m.y - a.y);
var pC = carre(m.x - a.x) + carre(m.y - a.y) - carre(rc) + carre(m.r);
var delta = carre(2 * pA * pC) - 4 * (carre(pA) + carre(pB)) * (carre(pC) - carre(pB) * carre(m.r));
var xP = a.x + ((2 * pA * pC - Math.sqrt(delta)) / (2 * (carre(pA) + carre(pB))));
var xQ = a.x + ((2 * pA * pC + Math.sqrt(delta)) / (2 * (carre(pA) + carre(pB))));
var yP = a.y + ((pC - pA * (xP-a.x)) / pB);
var yQ = a.y + ((pC - pA * (xQ-a.x)) / pB);
Je ne suis pas étudiant en BEP.
Bonjour bulldog33,
Je reprends ici la formule donnée plus bas par Ben314 (que j'ai vérifiée également), en la transcrivant sous forme de coordonnées.
Comme pour l'autre problème, prenons O au milieu de [AB] : et
et  . R est le rayon des cercles, AB =
. R est le rayon des cercles, AB = ^2+(y_a-y_b)^2})
Les points d'intersection M et P des 2 cercles de centres A et B sont (si ces cercles sont suffisamment proches) :
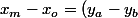 . \sqrt[2]{\frac{R^2}{AB^2}-\frac{1}{4}})
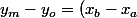 . \sqrt[2]{\frac{R^2}{AB^2}-\frac{1}{4}})
Tu en déduis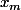 et
et 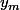 . Pour P, les formules sont les mêmes, sauf qu'il faut les multiplier par un "-". :lol3:
. Pour P, les formules sont les mêmes, sauf qu'il faut les multiplier par un "-". :lol3:
Je reprends ici la formule donnée plus bas par Ben314 (que j'ai vérifiée également), en la transcrivant sous forme de coordonnées.
Comme pour l'autre problème, prenons O au milieu de [AB] :
Les points d'intersection M et P des 2 cercles de centres A et B sont (si ces cercles sont suffisamment proches) :
Tu en déduis
34 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
