Démonstration aux consignes que j'ai peine à comprendre
38 messages
- Page 1 sur 2 - 1, 2
démonstration aux consignes que j'ai peine à comprendre
Bonjour.
Je ne suis pas en licence de math, j'ai fait un bac ES,
mais j'ai une passion pour les maths et donc je suis en train
de récupérer des fondations solides dans les diverses branches,
avec preuves et démonstrations rigoureuses, ce qui fait défaut je l'ai
vu à maintes cours de terminal.
j'essaie de comprendre la démonstration de l'existence de l'exponentielle.
J'utilise cette feuille : tsmaths.free.fr/Prepa/existenceexpo.pdf
Je ne comprend pas la phrase 2.3 "montrer qu'au-delà d'un certain rang, 'expression en question avec n et x ' est supérieure à -1
est-ce que cela veut dire : au delà d'un certain n, l'expression est supérieure à -1 pour tout x ?
Merci
Je ne suis pas en licence de math, j'ai fait un bac ES,
mais j'ai une passion pour les maths et donc je suis en train
de récupérer des fondations solides dans les diverses branches,
avec preuves et démonstrations rigoureuses, ce qui fait défaut je l'ai
vu à maintes cours de terminal.
j'essaie de comprendre la démonstration de l'existence de l'exponentielle.
J'utilise cette feuille : tsmaths.free.fr/Prepa/existenceexpo.pdf
Je ne comprend pas la phrase 2.3 "montrer qu'au-delà d'un certain rang, 'expression en question avec n et x ' est supérieure à -1
est-ce que cela veut dire : au delà d'un certain n, l'expression est supérieure à -1 pour tout x ?
Merci
paquito a écrit:Tout dépend de la façon dont on définit l'exponentielle:
normalement c'est à partir de
on peut envisager aussi
donc précise ce que tu utilises SVP.
L'objectif du problème est justement de définir l'exponentielle.
De plus la question posée ne dépend absolument pas de la façon dont ils la définissent.
En somme, en plus d'être désagréable, ta réponse est complètement hors de propos.
TS: On appelle fonction exp l'unique solution de y'-y=0 qui vérifie exp(0)=1 (résultat admis);
Je m'occupe d'handicapés qui ne savent pas exprimer correctement leur demande de façon bénévole, donc je ne te répondrais plus si tu ne t'excuses pas pour ta remarque stupide.
Ceci étant mis au point, je ne peut t'aider correctement que si je sais à quel niveau je peux me placer:
sup, spé, licence, etc...
Je m'occupe d'handicapés qui ne savent pas exprimer correctement leur demande de façon bénévole, donc je ne te répondrais plus si tu ne t'excuses pas pour ta remarque stupide.
Ceci étant mis au point, je ne peut t'aider correctement que si je sais à quel niveau je peux me placer:
sup, spé, licence, etc...
Alors,
1) La question posée ici est très claire, et j'y ai répondu.
2) Je n'ai pas besoin d'aide, je suis venu ici pour aider.
3) La ténacité dont tu fais preuve pour critiquer les remarques des autres (ici on a droit à un "stupide") dés qu'elles viennent te contredire, dénotant ton manque de recul par rapport aux choses me fait me demander quel intérêt de venir poster ici. Est ce que tu as ne serait ce que lu l'ensemble du message de l'auteur ? L'"handicapé" ici serait peut-être la personne incapable de trouver une question alors qu'elle est sous ses yeux.
1) La question posée ici est très claire, et j'y ai répondu.
2) Je n'ai pas besoin d'aide, je suis venu ici pour aider.
3) La ténacité dont tu fais preuve pour critiquer les remarques des autres (ici on a droit à un "stupide") dés qu'elles viennent te contredire, dénotant ton manque de recul par rapport aux choses me fait me demander quel intérêt de venir poster ici. Est ce que tu as ne serait ce que lu l'ensemble du message de l'auteur ? L'"handicapé" ici serait peut-être la personne incapable de trouver une question alors qu'elle est sous ses yeux.
Matt_01 a écrit:Ici c'est plutôt :
Pour ce x là, à partir d'un certain rang (par rapport à n), l'expression est supérieure à -1.
Donc la réponse est (elle est dans le document, mais ça n'a pas d'intérêt de regarder tout de suite),
en posant et résolvant simplement : n > -x - 1 pour un x donné.
Ai-je compris, au regard de la réponse donné ? je ne crois pas, à ce qu'elle me semble compliquée.
Pour l'info, mon niveau est entre seconde et et terminale.
Ne t'en fais pas pour l'autre rigolo ...
Merci
Merci Matt, et ne t'en fais pas pour l'autre. ca m'a bien fait rire au contraire.
La réponse donne en outre la condition que (n + x/n) > 0 ce que je ne comprend pas.
Mais à posteriori je me rend compte que j'ai commencé par le mauvais bon !
Cette preuve est presque trop dure pour une classe de terminal, alors je crois que c'est la part du programme que je ferai en dernier.
La réponse donne en outre la condition que (n + x/n) > 0 ce que je ne comprend pas.
Mais à posteriori je me rend compte que j'ai commencé par le mauvais bon !
Cette preuve est presque trop dure pour une classe de terminal, alors je crois que c'est la part du programme que je ferai en dernier.
Paquito : il y a un malentendu. Dans cette discussion il s'agit de construire l'exponentielle comme limite de la suite des ^n) . Cette définition, qui n'est pas la plus courante, a le mérite d'être abordable en début de bac+1 sans rien admettre. Je l'ai trouvé dans un livre de licence 1, mais c'est très calculatoire.
. Cette définition, qui n'est pas la plus courante, a le mérite d'être abordable en début de bac+1 sans rien admettre. Je l'ai trouvé dans un livre de licence 1, mais c'est très calculatoire.
(Les deux autres constructions courantes nécessitent soit d'admettre quelque chose, soit d'attendre bac+2. La définition par une série nécessite le cours des séries, donc bac+2, et la construction comme réciproque du logarithme nécessite l'existence du logarithme, donc d'admettre l'existence de primitives d'une fonction continue, ou bien de le démontrer, donc là encore plutôt bac+2.)
Bref, Matt_01 a parfaitement raison et tu étais hors-sujet.
(Les deux autres constructions courantes nécessitent soit d'admettre quelque chose, soit d'attendre bac+2. La définition par une série nécessite le cours des séries, donc bac+2, et la construction comme réciproque du logarithme nécessite l'existence du logarithme, donc d'admettre l'existence de primitives d'une fonction continue, ou bien de le démontrer, donc là encore plutôt bac+2.)
Bref, Matt_01 a parfaitement raison et tu étais hors-sujet.
Il faut d'abord démontrer que=(1+\frac{x}{n})^n) est convergente; si
est convergente; si c'est trivial; si
c'est trivial; si ) est décroissante minorée par 1 et quand
est décroissante minorée par 1 et quand 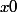 donc
donc ) devient croissante et majorée par 1, donc dans tous les cas
devient croissante et majorée par 1, donc dans tous les cas ) converge vers une fonction qu nous noterons exp(x).
) converge vers une fonction qu nous noterons exp(x).
=(1+\frac{x}{n})^{n-1})
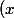)
^n(1+\frac{x}{n})^{-1}) et à la limite,tu obtient
et à la limite,tu obtient =exp(x)) On a
On a ) dérivable pour tout n et
dérivable pour tout n et^n(1+\frac{x}{n})^{-1}=lim_{n\to oo}=(1+\frac{x}{n})^n*lim_{n\to oo}=(1+\frac{x}{n})^{-1}=exp(x)) ; donc les suite
; donc les suite ) et
et) ont la même limite
ont la même limite ) , la convergence étant uniforme sur tout compact de
, la convergence étant uniforme sur tout compact de  , donc, on a construit une fonction, notée exp qui vérifie
, donc, on a construit une fonction, notée exp qui vérifie =exp) et
et =1) donc après tu démontre tout comme en TS (évidemment, ce n'est pas possible en TS, puisque l'on a besoin de la convergence uniforme:
donc après tu démontre tout comme en TS (évidemment, ce n'est pas possible en TS, puisque l'on a besoin de la convergence uniforme: -exp(x))->0)) ;
;
C'est plus simple avec les séries entières, mais on peut s'en sortir avec des fonctions polynômes qui sont biens sympathiques?
désolé pour hier, mais je n'avais pas le temps.
C'est plus simple avec les séries entières, mais on peut s'en sortir avec des fonctions polynômes qui sont biens sympathiques?
désolé pour hier, mais je n'avais pas le temps.
Pour pouvoir utiliser ce que tu viens d'écrire il faudrait montrer la convergence uniforme sur tout segment de u_n'.
Mais u_n'(x) est croissante à partir d'un certain rang (en n) et donc il suffit de montrer que la limite de u_n' est continue, pour pouvoir en déduire la convergence uniforme sur tout segment de u_n', et en déduire que la limite de u_n est dérivable et sa dérivée est la limite de un'.
En gros :
u_n converge. On montre que la limite u est continue.
u_n' converge vers u avec u_n croissante (en n) et u continue donc on a convergence uniforme sur tout segment et donc u est dérivable avec u'=u.
(Mais on utilise des notions non abordées en TS).
Le seul passage non traité est la continuité de u.
Et d'ailleurs, le poly d'evanescente résolu le problème sans considérer la suite des un', j'ai l'impression que tu ne l'as pas lu.
Mais u_n'(x) est croissante à partir d'un certain rang (en n) et donc il suffit de montrer que la limite de u_n' est continue, pour pouvoir en déduire la convergence uniforme sur tout segment de u_n', et en déduire que la limite de u_n est dérivable et sa dérivée est la limite de un'.
En gros :
u_n converge. On montre que la limite u est continue.
u_n' converge vers u avec u_n croissante (en n) et u continue donc on a convergence uniforme sur tout segment et donc u est dérivable avec u'=u.
(Mais on utilise des notions non abordées en TS).
Le seul passage non traité est la continuité de u.
Et d'ailleurs, le poly d'evanescente résolu le problème sans considérer la suite des un', j'ai l'impression que tu ne l'as pas lu.
Matt_01 a écrit:Pour pouvoir utiliser ce que tu viens d'écrire il faudrait montrer la convergence uniforme sur tout segment de u_n'.
Mais u_n'(x) est croissante à partir d'un certain rang (en n) et donc il suffit de montrer que la limite de u_n' est continue, pour pouvoir en déduire la convergence uniforme sur tout segment de u_n', et en déduire que la limite de u_n est dérivable et sa dérivée est la limite de un'.
En gros :converge. On montre que la limite u est continue.
u_n' converge vers u avec u_n croissante (en n) et u continue donc on a convergence uniforme sur tout segment et donc u est dérivable avec u'=u.
(Mais on utilise des notions non abordées en TS).
Le seul passage non traité est la continuité de u.
Et d'ailleurs, le poly d'evanescente résolu le problème sans considérer la suite des un', j'ai l'impression que tu ne l'as pas lu.
tu te place sur un compact
soit N le plus petit entier tel que u_n(x)>0; on suppose donc que n\geq N et soit n_0 donné; supposons que
Cela met en évidence une infinité de max pour une suite de fonctions polynômes qui converge simplement vers exp, ce qui me semble contradictoire.
Matt_01 a écrit:Pour pouvoir utiliser ce que tu viens d'écrire il faudrait montrer la convergence uniforme sur tout segment de u_n'.
Mais u_n'(x) est croissante à partir d'un certain rang (en n) et donc il suffit de montrer que la limite de u_n' est continue, pour pouvoir en déduire la convergence uniforme sur tout segment de u_n', et en déduire que la limite de u_n est dérivable et sa dérivée est la limite de un'.
En gros :
u_n converge. On montre que la limite u est continue.
u_n' converge vers u avec u_n croissante (en n) et u continue donc on a convergence uniforme sur tout segment et donc u est dérivable avec u'=u.
(Mais on utilise des notions non abordées en TS).
Le seul passage non traité est la continuité de u.
Et d'ailleurs, le poly d'evanescente résolu le problème sans considérer la suite des un', j'ai l'impression que tu ne l'as pas lu.
Une fonction continue n'est pas n'est pas forcément limite uniforme d'une suite de fonction continues!
paquito a écrit:est strictement monotone à partir d'un certain ce qui perment de montrer la convergence uniforme avec un petit raisonnement par l'absurde:
tu te place sur un compactet tu supposes qu'il existe un réel
tel que \
; tu dois aboutir à une contradiction; la suite
, suite de fonctions continues et dérivable sur K atteint aussi ses bornes;
soit N le plus petit entier tel que u_n(x)>0; on suppose donc que n\geq N et soit n_0 donné; supposons queréalise le max de u_n sur K; lorsque n croît,
ne peut rester le max très longtemps en raison de la convergence simple de notre suite; il faut donc envisager un entier
et un réel
, avec u_{n_1}(x_1)=lambda>=0.
Un exemple serait la suite u_n(x)=x^n sur [0,1] : la suite est monotone (au sens de n) et converge vers f qui vaut 1 en 1 et 0 sur le reste, et donc on n'a pas continuité uniforme vu qu'on perd la continuité (d'où l'importance de montrer la continuité de la fonction limite).Une fonction continue n'est pas n'est pas forcément limite uniforme d'une suite de fonction continues!
J'ai pas sous entendu ca, mais on a toujours, pour f donnée, la suite f_n=f qui converge uniformément vers f.
Pardon d'arriver après la bataille, mais ce passage:
me pose problème. Comment montrer que la suite converge?
J'ai l'impression que l'on utilise l'un des outils suivants:
-logarithme et développements limités (et voire même exponentielle!)
-complétude
Après j'ai bien une idée de preuve par complétude (mais alors c'est coton en L1) qui permet de définir le nombre , mais alors après les résultats de continuité (ne parlons pas de dérivabilité!) ça ma parait assez dur pour des L1 (majorations fines...).
, mais alors après les résultats de continuité (ne parlons pas de dérivabilité!) ça ma parait assez dur pour des L1 (majorations fines...).
Bref, si quelqu'un a une référence, je suis preneur.
Cordialement
Robic a écrit:Paquito : [...] Dans cette discussion il s'agit de construire l'exponentielle comme limite de la suite des. Cette définition, qui n'est pas la plus courante, a le mérite d'être abordable en début de bac+1 sans rien admettre. Je l'ai trouvé dans un livre de licence 1, mais c'est très calculatoire.
[...]
me pose problème. Comment montrer que la suite converge?
J'ai l'impression que l'on utilise l'un des outils suivants:
-logarithme et développements limités (et voire même exponentielle!)
-complétude
Après j'ai bien une idée de preuve par complétude (mais alors c'est coton en L1) qui permet de définir le nombre
Bref, si quelqu'un a une référence, je suis preneur.
Cordialement
Salut Matt
je n'ai jamais vu la fonction exponentielle définie à partir de=(1+\frac{x}{n})^n) , et pour cause c'est un vrai merdier; par contre lorsque l'on a défini autrement la fonction exp, le logarithme vient très vite et on arrive aussitôt à
, et pour cause c'est un vrai merdier; par contre lorsque l'on a défini autrement la fonction exp, le logarithme vient très vite et on arrive aussitôt à ^n=exp(x)) , résultat qui sert beaucoup.
, résultat qui sert beaucoup.
Sinon si tu as une suite de fonction) définies sur un compact (ce n'est pas une obligation), si pour tout x fixé
définies sur un compact (ce n'est pas une obligation), si pour tout x fixé) a une limite
a une limite) ,
,  converge simplement vers f, mais f n'est pas forcément continue ou dérivable et l'intégrale de f n'est pas forcément la limite de l'intégrale de
converge simplement vers f, mais f n'est pas forcément continue ou dérivable et l'intégrale de f n'est pas forcément la limite de l'intégrale de  . Sinon on se ramène toujours vers la convergence vers la fonction nulle en posant
. Sinon on se ramène toujours vers la convergence vers la fonction nulle en posant=u_n(x)-f(x))
Exemples:
= x^n-(1-x)^n) (la limite simple n'est pas continue.)
(la limite simple n'est pas continue.)
=x^n-x^{2n}) (phénomène de la bosse glissante; f est continue et dérivable)
(phénomène de la bosse glissante; f est continue et dérivable)
Et il y a plein d autres contre-exemples dont ta suite qui doit converger uniformément sur tout compact, ce que je n'arrive pas à prouver (l'infinité de max ne prouve pas que ces max tendent vers 0)
Donc je te montrerais quand même comment on fait d'habitude, ce problème étant en fait original.
je n'ai jamais vu la fonction exponentielle définie à partir de
Sinon si tu as une suite de fonction
Exemples:
Et il y a plein d autres contre-exemples dont ta suite qui doit converger uniformément sur tout compact, ce que je n'arrive pas à prouver (l'infinité de max ne prouve pas que ces max tendent vers 0)
Donc je te montrerais quand même comment on fait d'habitude, ce problème étant en fait original.
SLA a écrit:Pardon d'arriver après la bataille, mais ce passage:
me pose problème. Comment montrer que la suite converge?
J'ai l'impression que l'on utilise l'un des outils suivants:
-logarithme et développements limités (et voire même exponentielle!)
-complétude
Après j'ai bien une idée de preuve par complétude (mais alors c'est coton en L1) qui permet de définir le nombre, mais alors après les résultats de continuité (ne parlons pas de dérivabilité!) ça ma parait assez dur pour des L1 (majorations fines...).
Bref, si quelqu'un a une référence, je suis preneur.
Cordialement
Salut SLA,
J'y connais pas grand chose mais je me rappelle d'un doc à destination des TS (mais un peu dur) ou on introduit la suite
Si tu veux la ref, je peux te la retrouver :lol3:
38 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
