Integrale Stokes

[Vitlia]

Bonjour je dois resoudre un exercice mais je dois avouer que je suis un peu perdu le voici:

Soient S={(x,y,z) E R3 : x^2+4*y^2+z^2=1 , y >= 1/4 } , la fonction F tel que F E C1(R3,R3) , v est le vecteur normal de S tel que v(0,1/2,0)=(0,1,0).

Exercice: transformer l'integrale de Stokes sur l'ensemble S en un integrale simple entre [0,2pi]

Votre aide est la bienvenue je vous remercie d'avance !

Ps: j'ai utilisé ''E'' pour dire ''appartient''

[Pythales]

Bonjour je dois resoudre un exercice mais je dois avouer que je suis un peu perdu le voici:

Soient S={(x,y,z) E R3 : x^2+4*y^2+z^2=1 , y >= 1/4 } , la fonction F tel que F E C1(R3,R3) , v est le vecteur nomal de S tel que v(0,1/2,0)=(0,1,0).

Exercice: transformer l'integrale de Stokes sur l'ensemble S en un integrale simple entre [0,2pi]

Votre aide est la bienvenue je vous remercie d'avance !

Ps: j'ai utilisé ''E'' pour dire ''appartient''

Incompréhensible !
De quel vecteur s'agit-il ?
La formule de Stokes transforme une intégrale curviligne (circulation d'un vecteur) en une intégrale double (flux de son rotationnel).
C'est plutôt dans le sens simple vers double qu'elle est utilisée.
Précise ton problème.

[Ben314]

Salut,
J'aurais tendance à penser que, vu le contexte, il s'agit de la version "physicienne" du théorème de Stokes dans R^3 :

et qu'il faut expliciter le terme de droite dans le cas de la surface S orientée par v de son post (tout en gardant F "tel quel" vu qu'on le connait pas)

Mais c'est pas forcément ça...

[Vitlia]

Est-il possible d'insérer une image depuis les fichiers d'un ordinateur ? (Comme ca je pourrais vous faire voir l'exercice directement)

[Vitlia]

Mais oui effectivement Ben314 l'exercice se fait dans la version "physicienne" en gardant F tel quel car il n'est pas exprimé.

[Ben314]

Dans ce cas, ça se résume quasi uniquement à trouver une paramétrisation de dont l'orientation soit "issue" de l'orientation de S (a mon sens c'est LE truc un peu chiant de l'exo.).

Tu vois ce que c'est S ? (si tu ne "vois" rien, il y a une paramétrisation archi. classique)
et tu vois ce que c'est ?

[Vitlia]

Et bien l'ensemble S est la surface d'une sphère je pense.

[Ben314]

Et bien l'ensemble S est la surface d'une sphère je pense.

Presque, mais pas tout à fait...

[Vitlia]

Presque, mais pas tout à fait...

Une espèce de sphère ''écrasée''

[DamX]

Une espèce de sphère ''écrasée''

Hello,

Oui le x^2+4*y^2+z^2=1 te donne une sphère "écrasée", mais la définition comporte aussi la condition y >= 1/4. Du coup le résultat n'est pas une sphère écrasée telle quelle, mais c'est .. ? ce qui du coup te donne comme frontière de ta surface la courbe .. ?

Damien

[Vitlia]

Un ''dome'' (la portion de la sphère écrasée ''au dela'' de y=1/4)

[DamX]

exact, donc la frontière (le "bord") c'est quoi ?
tu peux la paramétriser comment (pour en revenir à la question initiale) ?

[Pythales]

Bonjour je dois resoudre un exercice mais je dois avouer que je suis un peu perdu le voici:

Soient S={(x,y,z) E R3 : x^2+4*y^2+z^2=1 , y >= 1/4 } , la fonction F tel que F E C1(R3,R3) , v est le vecteur normal de S tel que v(0,1/2,0)=(0,1,0).

Exercice: transformer l'integrale de Stokes sur l'ensemble S en un integrale simple entre [0,2pi]

Votre aide est la bienvenue je vous remercie d'avance !

Ps: j'ai utilisé ''E'' pour dire ''appartient''

Sauf erreur, si je comprends bien, a pour composantes et il s'agit de déterminer les composantes d'un vecteur dont serait le rotationnel

[Vitlia]

On peut peut etre paramétriser comme ca :

x=cos(a)cos(b)
y=(1/2)cos(a)sin(b)
z=sin(a)

(je ne suis pas sur du tout...)

[Pythales]

On peut peut etre paramétriser comme ca :

x=cos(a)cos(b)
y=(1/2)cos(a)sin(b)
z=sin(a)

(je ne suis pas sur du tout...)

Moi j'aurais posé



de telle sorte que la courbe a pour équation

[Ben314]

Sauf erreur, si je comprends bien, a pour composantes et il s'agit de déterminer les composantes d'un vecteur dont serait le rotationnel

non, si M est un point de la surface, v(M) c'est le vecteur normal unitaire (a mon avis vu l'article LE placé devant) à la surface et dans l'exo., il ne sert qu'à une seule chose, c'est à préciser la façon dont la surface est orienté de façon à savoir comment on doit orienter son bord.
Plus précisément la formule v(0,1/2,0)=(0,1,0) te dit juste que la portion d'ellipsoïde considérée est orientée positivement du coté extérieur de ellipsoïde donc qu'il faut regarder la surface "depuis les grand y en regardant vers 0" et que le cercle bordant la surface devra être orienté dans le sens trigo. lorsqu'il est vu par ce coté là.


Edit : Et je me demande si justement ta paramétrisation ne tourne pas dans le mauvais sens (tu as calculé le vecteur normal correspondant à la paramétrisation de ta surface pour voir si c'était le bon ?)

[Pythales]

non, si M est un point de la surface, v(M) c'est le vecteur normal unitaire (a mon avis vu l'article LE placé devant) à la surface et dans l'exo., il ne sert qu'à une seule chose, c'est à préciser la façon dont la surface est orienté de façon à savoir comment on doit orienter son bord.
Plus précisément la formule v(0,1/2,0)=(0,1,0) te dit juste que la portion d'ellipsoïde considérée est orientée positivement du coté extérieur de ellipsoïde donc qu'il faut regarder la surface "depuis les grand y en regardant vers 0" et que le cercle bordant la surface devra être orienté dans le sens trigo. lorsqu'il est vu par ce coté là.


Edit : Et je me demande si justement ta paramétrisation ne tourne pas dans le mauvais sens (tu as calculé le vecteur normal correspondant à la paramétrisation de ta surface pour voir si c'était le bon ?)

Alors là, je ne comprends plus quel est le problème.
J'avais cru comprendre qu'il s'agissait de transformer une intégrale double (flux d'un rotationnel à travers l'ellipsoïde) en une intégrale simple (circulation d'un vecteur le long de la courbe limitant l'ellipsoïde), le rotationnel étant précisément le vecteur v, normal à la surface.
Le problème se limitait alors à déterminer quel était le vecteur U dont V était le rotationnel, puis de calculer la circulation de ce vecteur U le long de la courbe limitant la surface.

Mais j'ai certainement dû me tromper ...

[DamX]

Alors là, je ne comprends plus quel est le problème.
J'avais cru comprendre qu'il s'agissait de transformer une intégrale double (flux d'un rotationnel à travers l'ellipsoïde) en une intégrale simple (circulation d'un vecteur le long de la courbe limitant l'ellipsoïde), le rotationnel étant précisément le vecteur v, normal à la surface.
Le problème se limitait alors à déterminer quel était le vecteur U dont V était le rotationnel, puis de calculer la circulation de ce vecteur U le long de la courbe limitant la surface.

Mais j'ai certainement dû me tromper ...

On cherche bien à intégrer un rotationnel, mais c'est le rotationnel de F (voir 1er post de Ben), que l'on ne connaît pas et n'a pas besoin de connaître.
Le vecteur V normal à la surface qui est donné permet seulement d'orienter la surface, et du coup après avoir utilisé le théorème de Stokes, oriente le bord (le cercle d'axe Oy, avec y=1/4 et de rayon 3/4) qui est le domaine d'intégration pour la circulation du champ de vecteur F sur le bord de la surface (membre de droite de l'équation). Le sens de la normale V modifie donc juste le signe du résultat.
Je n'ai fait que paraphraser Ben.

Et je suis d'accord avec son orientation, dans le sens contraire de la tienne pour la paramétrisation du cercle, que l'on peut retrouver en jouant avec ses doigts (c'est pratique la physique ! :++: )

Damien

[Ben314]

C'est bien ça la question, mais le vecteur (variable) dont on doit calculer le flux du rotationnel à travers la surface et/ou la circulation le long de la courbe bordant la surface, dans l'énoncé, c'est la "fonction F" qui est elle complètement inconnue.

Le petit problème ici, c'est que pour pouvoir calculer un flux à travers une surface il faut que la surface soit orientée (pour différencier le flux "entrant" du flux "sortant") et de même, pour calculer la circulation le long d'une courbe, il faut que la courbe soit orientée.
Et si on veut que la formule de Stokes soit vérifiée non seulement en valeur absolue, mais qu'on ait le même signe pour les deux intégrales, il faut que l'orientation de la surface et de son bord soit "cohérente" l'une avec l'autre.

Donc dans l'exo, pour que tu n'ait pas le choix concernant l'orientation que tu va prendre pour le cercle qui borde S, on te donne l'orientation qui a été choisie pour S. Et choisir l'orientation d'une surface, ça revient à choisir parmi les deux candidats possibles qui on prend comme vecteur normal unitaire à la surface qui va, par définition, être considéré comme le "vecteur sortant" de la surface (et, évidement, si la surface est connexe, il suffit de préciser quel est le "vecteur sortant" en un point de la surface pour en déduire l'orientation).

Donc, toujours dans cet exo, comme l'équation de la surface S est , l'équation du plan tangent en un point est 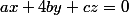donc en particulier, l'équation du plan tangent en en est de vecteur normal unitaire et l'énoncé te dit qu'on oriente la surface en choisissant comme "vecteur sortant" au point (0,1/2,0) le vecteur (0,1,0) et donc comme "vecteur rentrant" le vecteur (0,-1,0).
C'est avec cette info là que tu doit déduire quelle est l'orientation qu'il faut prendre pour le cercle , c'est à dire est-ce qu'il faut paramétré par ou bien par ?

Sauf erreur, c'est la deuxième solution.


Edit : j'ai pas vu le post de DamX d'où... forte redite...

[Ben314]

Sinon, si ça t'intéresse de le faire avec du calculs et pas avec des arguments visuels du style "ça doit tourner dans le sens trigo. quand on regarde par le coté extérieur" ou bien les fameuse "règle des 3 doigts" (sans doute plus classique pour un physicien, sauf que je sais jamais quel doigt représente quoi... ), on part d'une paramétrisation de la surface, par exemple la tienne :

En précisant et pour parcourir une fois et une seule la surface S donnée.
On calcule les dérivées partielles et puis le vecteur normal unitaire .
En et , ça donne ce qui signifie que la paramétrisation oriente la surface à l'opposé de ce qui est demandé par l'énoncé.
Donc une paramétrisation orientant correctement la surface est, par exemple, (qui échange les termes du produit vectoriel)
Maintenant, si on regarde dans R² le bord du rectangle (avec en premier et en deuxième) que l'on parcours dans le sens trigo, le bord correspondant à 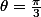est parcouru de à (les 3 autres bords du rectangle correspondent à un "aller retour" sur un arc de la surface donc ne correspondent pas au "bord" de la surface).
Donc ta paramétrisation du bord est correcte à condition d'intégrer le flux de à et pas de 0 à (ce qui change le signe de l'intégrale)

Evidement, le bilan, c'est qu'il est clairement plus rapide d'utiliser des arguments "visuels"... :doh: